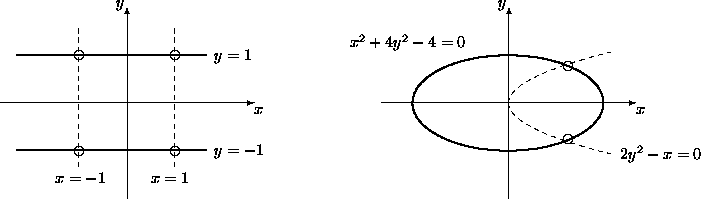The classical convex-linear homotopy that connects target with start system is
![\begin{displaymath}
H(x,y,t) =
(1 - t) \gamma \left(
\underbrace{\overbrace{\...
...ght.}^{target}}_{F(x,y) = {\bf 0}}
\right), \quad t \in [0,1].\end{displaymath}](img36.gif) |
(9) |
By choosing a random complex number 
, we can reach all
complex solutions even when all start solutions are real,
see Figure 7.
At t=0 we have the degenerate configuration which is trivial to solve.
By following the solution paths defined by the homotopy we arrive for t = 1 at two real and two complex conjugated solutions of the target system. Note that in the x-component we have only two different paths.
It is recommended to put the algebraic formulation in a file to avoid typing it over many times. The file mickey of the demonstration database starts as follows
2
x**2 + 4*y**2 - 4;
2*y**2 - x;
By typing phc -b mickey /tmp/mickey.bphc the black-box solver is invoked. The result can be seen in the file /tmp/mickey.bphc.
Next a session with phc in full mode is represented choosing default options.
your_machine_prompt: phc mickey /tmp/mickey.phc
Welcome to PHC (Polynomial Homotopy Continuation) Version 2.0.
Running in full mode. Note also the following options:
phc -s : Equation and variable Scaling on system and solutions
phc -d : Linear and nonlinear Reduction w.r.t. the total degree
phc -r : Root counting and Construction of start systems
phc -m : Mixed-Volume Computation by four lifting strategies
phc -p : Polynomial Continuation by a homotopy in one parameter
phc -v : Validation, refinement and purification of solutions
phc -e : SAGBI homotopies for a problem in enumerative geometry
phc -b : Batch or black-box processing
MENU for Scaling Polynomial Systems :
0 : No Scaling : leave the menu
1 : Equation Scaling : divide by average coefficient
2 : Variable Scaling : change of variables, as z = (2^c)*x
Type 0, 1, or 2 to select scaling, or i for info : 0
MENU for Reducing Polynomial Systems :
0 : No Reduction : leave the menu
1 : Linear Reduction : triangulate coefficient matrix
2 : Sparse Linear Reduction : diagonalize coefficient matrix
3 : Nonlinear Reduction : S-polynomial combinations
Type 0, 1, 2, or 3 to select reduction, or i for info : 0
MENU with ROOT COUNTS and Methods to Construct START SYSTEMS :
0. exit - current start system is based on total degree : 4
PRODUCT HOMOTOPIES based on DEGREES ------------------------------
1. multi-homogeneous Bezout number (one partition)
2. partitioned linear-product Bezout number (many partitions)
3. general linear-product Bezout number (set structure)
4. symmetric general linear-product Bezout number (group action)
POLYHEDRAL HOMOTOPIES based on NEWTON POLYTOPES ------------------
5. combination between Bezout and BKK Bound (implicit lifting)
6. mixed-volume computation (static lifting)
7. incremental mixed-volume computation (dynamic lifting)
8. symmetric mixed-volume computation (symmetric lifting)
START SYSTEM DEFINED BY USER -------------------------------------
9. you can give your own start system
Type a number between 0 and 9, eventually preceded by i for info : 0
Homotopy is H(x,t) = a*(1-t)^k * Q(x) + t^k * P(x) = 0, t in [0,1],
with Q(x) = 0 a start system, and P(x) = 0 the target system.
MENU with settings for homotopy :
relaxation constant k : 2
regularity constant a : 9.95793808261866E-01 9.16225486838865E-02
target value for t : 1.00000000000000E+00 0.00000000000000E+00
projective transformation : no
Type k, a, t, or p to change, preceded by i for info. Type 0 to exit : 0
****************** CURRENT CONTINUATION PARAMETERS *****************
GLOBAL MONITOR :
1. the condition of the homotopy : 0
2. number of paths tracked simultaneously : 1
3. maximum number of steps along a path : 500
4. distance from target to start end game : 1.000E-01
5. order of extrapolator in end game : 0
6. maximum number of re-runs : 1
STEP CONTROL (PREDICTOR) : along path : end game
7: 8. type ( x:Sec,t:Rea ):( x:Sec,t:Rea ) : 0 : 0
9:10. minimum step size : 1.000E-06 : 1.000E-08
11:12. maximum step size : 1.000E-01 : 5.000E-02
13:14. reduction factor for step size : 7.000E-01 : 5.000E-01
15:16. expansion factor for step size : 1.250E+00 : 1.100E+00
17:18. expansion threshold : 1 : 1
PATH CLOSENESS (CORRECTOR) : along path : end game
19:20. maximum number of iterations : 4 : 4
21:22. relative precision for residuals : 1.000E-09 : 1.000E-11
23:24. absolute precision for residuals : 1.000E-09 : 1.000E-11
25:26. relative precision for corrections : 1.000E-09 : 1.000E-11
27:28. absolute precision for corrections : 1.000E-09 : 1.000E-11
SOLUTIONS (TOLERANCES): along path : end game
29:30. inverse condition of Jacobian : 1.000E-04 : 1.000E-12
31:32. clustering of solutions : 1.000E-04 : 1.000E-12
33:34. solution at infinity : 1.000E+04 : 1.000E+12
********************************************************************
Type a number to change (0 to exit), preceded by i for info : 0
MENU for Output Information during Continuation :
0 : no intermediate output information during continuation
1 : only the final solutions at the end of the paths
2 : intermediate solutions at each step along the paths
3 : information of the predictor: t and step length
4 : information of the corrector: corrections and residuals
5 : intermediate solutions and information of the predictor
6 : intermediate solutions and information of the corrector
7 : information of predictor and corrector
8 : intermediate solutions, info of predictor and corrector
Type a number between 0 and 8 to select output information : 0
No more input expected. See output file for results.
your_machine_prompt:
In full mode, the program runs through the scaling and reduction menu, shows the user all root-counting possibilities and, after the choice of start system, invokes the polynomial continuation.