Introduction to OpenMP¶
Although the focus of this lecture is on OpenMP, we start out by introducing the running example, and by illustrating its multithreaded solution in Julia.
multithreading in Julia¶
The composite trapezoidal rule is defined in the Julia function below.
"""
function traprule(f::Function,
a::Float64, b::Float64,
n::Int)
returns the composite trapezoidal rule to
approximate the integral of f over [a,b]
using n function evaluations.
"""
function traprule(f::Function,
a::Float64, b::Float64,
n::Int)
h = (b-a)/n
y = (f(a) + f(b))/2
x = a + h
for i=1:n-1
y = y + f(x)
x = x + h
end
return h*y
end
The program continues below, with the use of Threads.
using Printf
using Base.Threads
nt = nthreads()
println("The number of threads : $nt")
subapprox = zeros(nt)
f(x) = sqrt(1 - x^2)
dx = 1/nt
bounds = [i for i=0:dx:1]
timestart = time()
@threads for i=1:nt
subapprox[i] = traprule(f, bounds[i], bounds[i+1], 1_000_000)
end
approxpi = 4*sum(subapprox)
elapsed = time() - timestart
println("The approximation for Pi : $approxpi")
err = @sprintf("%.3e", pi - approxpi)
println("with error : $err")
println("The elapsed time : $elapsed seconds")
Observe that in the parallel loop, every thread using one million function evaluations. Instead of a speedup, we should look for a quality up, and observe that the error of the approximation for \(pi\) decreases when using more threads.
To execute the code, at the command prompt in Linux, type
JULIA_NUM_THREADS=8 julia mtcomptrap.jl
to run the code with 8 threads.
As an alternative to setting the environment variable
JULIA_NUM_THREADS, launch the program as
julia -t 8 mtcomptrap.jl
to use 8 threads.
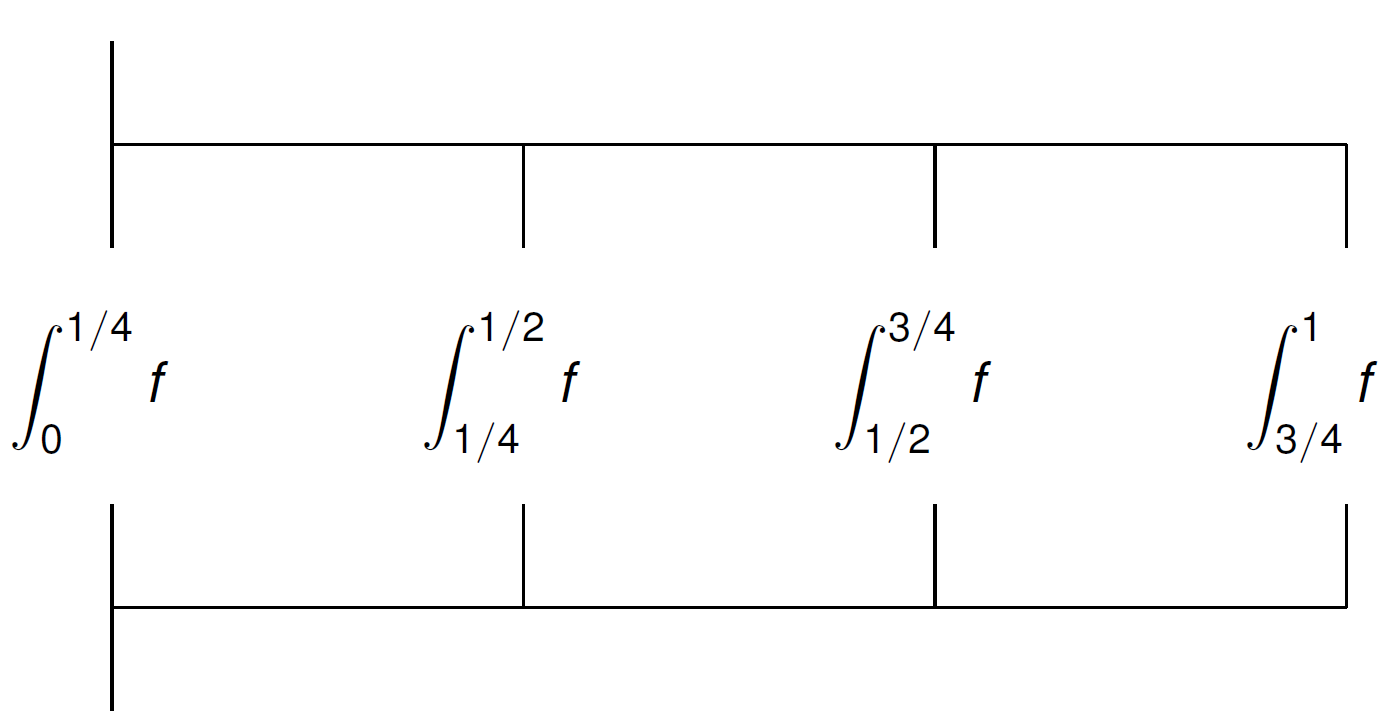
To introduce the notion of parallel region, consider the sequence Fig. 28. Suppose \(a_1, a_2, a_3\) can be executed in parallel, and similarly for the execution of \(b_1, b_2, b_3, b_4\), and \(c_1, c_2, c_3\).
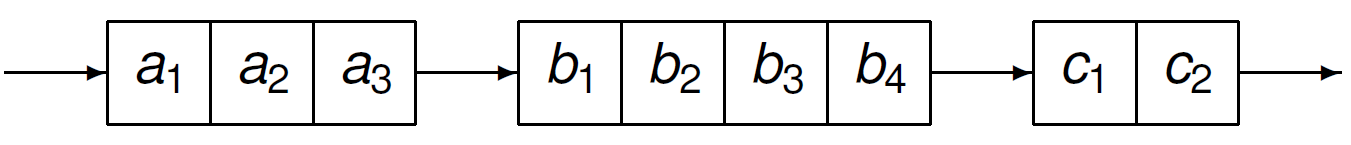
Fig. 28 A sequence of three blocks of statements.¶
The parallel execution of the sequence in Fig. 28 is shown in in Fig. 29.
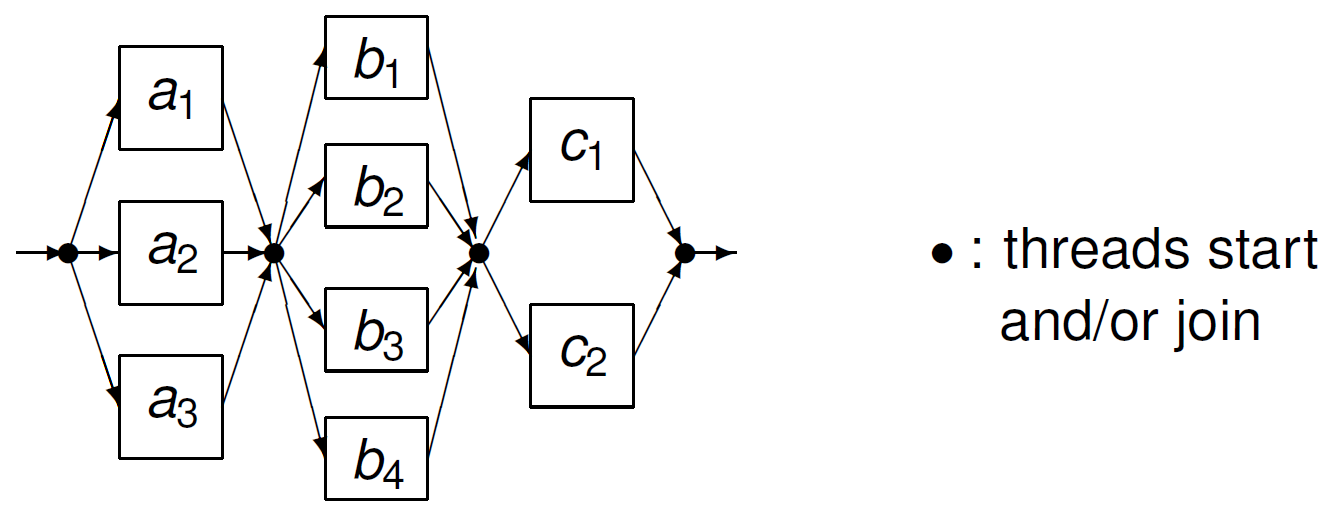
Fig. 29 Three parallel regions to execute a sequence of statements.¶
The running of a crew of four threads using three parallel regions is illustrated in Fig. 30.
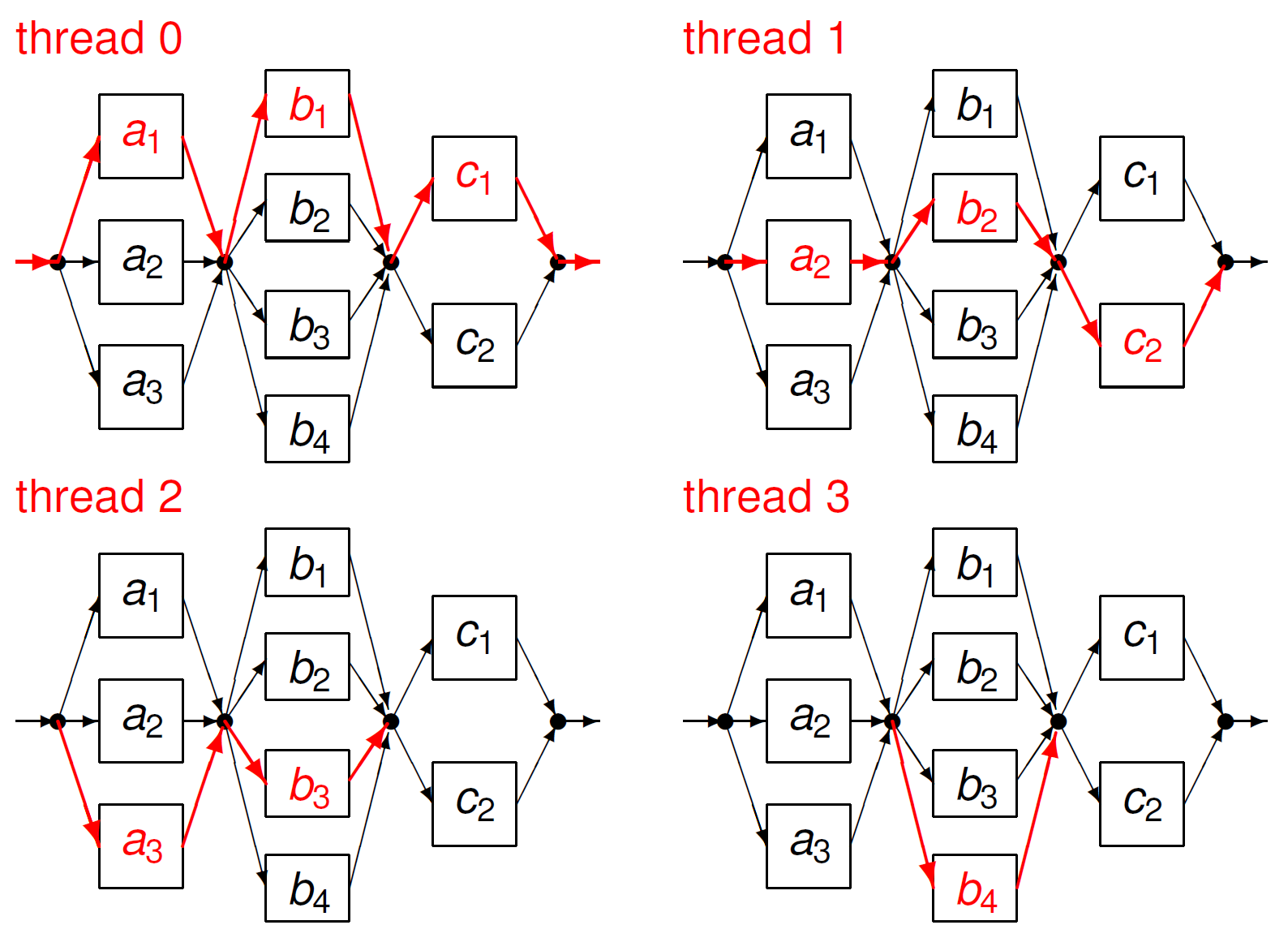
Fig. 30 Running a crew of four threads with three parallel regions.¶
the OpenMP Application Program Interface¶
OpenMP is an Application Program Interface which originated when a group of parallel computer vendors joined forces to provide a common means for programming a broad range of shared memory parallel computers.
The collection of
compiler directives (specified by
#pragma)library routines (call
gcc -fopenmp) e.g.: to get the number of threads; andenvironment variables (e.g.: number of threads, scheduling policies)
defines collectively the specification of the OpenMP API for shared-memory parallelism in C, C++, and Fortran programs. OpenMP offers a set of compiler directives to extend C/C++. The directives can be ignored by a regular C/C++ compiler…
With MPI, we identified processors with processes:
in mpirun -p as p is larger than
the available cores, as many as p processes are spawned.
In comparing a process with a thread, we can consider
a process as a completely separate program
with its own variables and memory allocation.
Threads share the same memory space
and global variables between routines.
A process can have many threads of execution.
using OpenMP¶
Our first program with OpenMP is below, Hello World!.
#include <stdio.h>
#include <omp.h>
int main ( int argc, char *argv[] )
{
omp_set_num_threads(8);
#pragma omp parallel
{
#pragma omp master
{
printf("Hello from the master thread %d!\n", omp_get_thread_num());
}
printf("Thread %d says hello.\n", omp_get_thread_num());
}
return 0;
}
If we save this code in the file hello_openmp0,
then we compile and run the program as shown below.
$ make hello_openmp0
gcc -fopenmp hello_openmp0.c -o /tmp/hello_openmp0
$ /tmp/hello_openmp0
Hello from the master thread 0!
Thread 0 says hello.
Thread 1 says hello.
Thread 2 says hello.
Thread 3 says hello.
Thread 4 says hello.
Thread 5 says hello.
Thread 6 says hello.
Thread 7 says hello.
$
Let us go step by step through the hello_openmp0.c program
and consider first the use of library routines.
We compile with gcc -fopenmp and put
#include <omp.h>
at the start of the program.
The program hello_openmp0.c uses two OpenMP library routines:
void omp_set_num_threads ( int n );sets the number of threads to be used for subsequent parallel regions.
int omp_get_thread_num ( void );returns the thread number, within the current team, of the calling thread.
We use the parallel construct as
#pragma omp parallel
{
S1;
S2;
...
Sm;
}
to execute the statements S1, S2, …, Sm in parallel.
The master construct specifies a structured block
that is executed by the master thread of the team.
The master construct is illustrated below:
#pragma omp parallel
{
#pragma omp master
{
printf("Hello from the master thread %d!\n", omp_get_thread_num());
}
/* instructions omitted */
}
The single construct specifies that the associated block is executed
by only one of the threads in the team (not necessarily the master thread),
in the context of its implicit task.
The other threads in the team, which do not execute the block,
wait at an implicit barrier at the end of the single construct.
Extending the hello_openmp0.c program with
#pragma omp parallel
{
/* instructions omitted */
#pragma omp single
{
printf("Only one thread %d says more ...\n", omp_get_thread_num());
}
}
Numerical Integration with OpenMP¶
We consider the composite trapezoidal rule for \(\pi\) via \(\displaystyle \frac{\pi}{4} = \int_0^1 \sqrt{1-x^2} dx\). The trapezoidal rule for \(f(x)\) over \([a,b]\) is \(\displaystyle \int_a^b f(x) dx \approx \frac{b-a}{2} (f(a) + f(b))\).
Using \(n\) subintervals of \([a,b]\):
The first argument of the C function for the composite
trapezoidal rule is the function that defines the integrand f.
The complete C program follows.
double traprule
( double (*f) ( double x ), double a, double b, int n )
{
int i;
double h = (b-a)/n;
double y = (f(a) + f(b))/2.0;
double x;
for(i=1,x=a+h; i < n; i++,x+=h) y += f(x);
return h*y;
}
double integrand ( double x )
{
return sqrt(1.0 - x*x);
}
int main ( int argc, char *argv[] )
{
int n = 1000000;
double my_pi = 0.0;
double pi,error;
my_pi = traprule(integrand,0.0,1.0,n);
my_pi = 4.0*my_pi; pi = 2.0*asin(1.0); error = my_pi-pi;
printf("Approximation for pi = %.15e with error = %.3e\n", my_pi,error);
return 0;
}
On one core at 3.47 Ghz, running the program evaluates \(\sqrt{1-x^2}\) one million times.
$ time /tmp/comptrap
Approximation for pi = 3.141592652402481e+00 with error = -1.187e-09
real 0m0.017s
user 0m0.016s
sys 0m0.001s
The private clause of parallel is illustrated below.
int main ( int argc, char *argv[] )
{
int i;
int p = 8;
int n = 1000000;
double my_pi = 0.0;
double a,b,c,h,y,pi,error;
omp_set_num_threads(p);
h = 1.0/p;
#pragma omp parallel private(i,a,b,c)
/* each thread has its own i,a,b,c */
{
i = omp_get_thread_num();
a = i*h;
b = (i+1)*h;
c = traprule(integrand,a,b,n);
#pragma omp critical
/* critical section protects shared my_pi */
my_pi += c;
}
my_pi = 4.0*my_pi; pi = 2.0*asin(1.0); error = my_pi-pi;
printf("Approximation for pi = %.15e with error = %.3e\n",my_pi,error);
return 0;
}
A private variable is a variable in a parallel region providing access to a different block of storage for each thread.
#pragma omp parallel private(i,a,b,c)
/* each thread has its own i,a,b,c */
{
i = omp_get_thread_num();
a = i*h;
b = (i+1)*h;
c = traprule(integrand,a,b,n);
Thread i integrates from a to b,
where h = 1.0/p and stores the result in c.
The critical construct restricts execution of the associated
structured block in a single thread at a time.
#pragma omp critical
/* critical section protects shared my_pi */
my_pi += c;
A thread waits at the beginning of a critical section
until no threads is executing a critical section.
The critical construct enforces exclusive access.
In the example, no two threads may increase my_pi
simultaneously. Running on 8 cores:
$ make comptrap_omp
gcc -fopenmp comptrap_omp.c -o /tmp/comptrap_omp -lm
$ time /tmp/comptrap_omp
Approximation for pi = 3.141592653497455e+00 \
with error = -9.234e-11
real 0m0.014s
user 0m0.089s
sys 0m0.001s
$
Compare on one core (error = -1.187e-09):
real 0m0.017s
user 0m0.016s
sys 0m0.001s
The results are summarized in Table 14. Summarizing the results:
real time |
error |
|
|---|---|---|
1 thread |
0.017s |
-1.187e-09 |
8 threads |
0.014s |
-9.234e-11 |
In the multithreaded version, every thread uses 1,000,000 subintervals. The program with 8 threads does 8 times more work than the program with 1 thread.
In the book by Wilkinson and Allen, section 8.5 is on OpenMP.
Bibliography¶
Barbara Chapman, Gabriele Jost, and Ruud van der Pas. Using OpenMP: Portable Shared Memory Parallel Programming. The MIT Press, 2007.
OpenMP Architecture Review Board. OpenMP Application Program Interface. Version 4.0, July 2013. Available at <http://www.openmp.org>.
Exercises¶
Read the first chapter of the book Using OpenMP by Chapman, Jost, and van der Pas.
Modify the
hello world!program with OpenMP so that the master thread prompts the user for a name which is used in the greeting displayed by thread 5. Note that only one thread, the one with number 5, greets the user.Modify the
hello world!program so that the number of threads is entered at the command line.Consider the Monte Carlo simulations we have developed with MPI for the estimation of \(\pi\). Write a version with OpenMP and examine the speedup.
Write an OpenMP program to simulate the management of a bank account, with the balance represented by a single shared variable. The program has two threads. Each thread shows the balance to the user and prompts for a debit (decrease) or a deposit (increase). Each thread then updates the balance in a critical section and displays the final the balance to the user.