Julia Sets of special rational maps
Julia sets are the chaotic domain of iterated complex functions that maps the to complex plane to itself. Notice the fractal sturcture of the boundary of the colored region, this boundary is the Julia set! For the following two functions as lambda goes to zero the Julia set becomes a space filling fractal curve giving a better and better approximation of the lambda=0 case (in the Hausdorff sense).
| Perturbed Basicila: f(z)=z^2-1+lambda/z^2 |
Basilica |
|

lambda=0.1
|

lambda=0.01
|

lambda=0.001
|

lambda=0
|
| Perturbed Douady Rabbit: f(z)=z^2+(-0.123+0.745i)+lambda/z^2 |
Douady Rabbit |
|
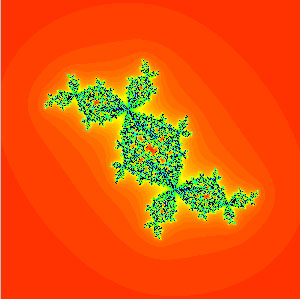
lambda=0.01
|

lambda=0.001
|

lambda=0.0001
|

lambda=0
|
You can read more about the dymamics of these particular maps here (undergrads may understand this) and here (advanced). For some accessible background and interactive media on complex dynamics take a look at the
Mandelbrot Set Explorer and
Bob Devaney's webpage. | 






