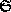Our program supports three different models to represent the structure of the system. First we can model the structure by a partition of the set of unknowns. Second, we can use a tuple of partitions, so that every equation can have a different partition. The most general model is a set structure, illustrated hereafter.
In (8) we show a supporting set structure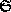 
for an example.
Based on 
we formally calculate the
number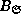 
as
The sets underneath the formula (9) indicate the sets
associated to the linear systems that determine the start solutions.
We proved that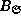 
actually bounds the number of
isolated complex solutions using a homotopy continuation argument.
Note that the total degree equals nine for this example.
The program provides for all models heuristic procedures for setting up a partition, tuple of partitions or set structure. Restricting to partitions, the user may ask to generate all partitions. Up to dimension eight, this is not too exhaustive in computational time. Following [26], the Bézout numbers are calculated efficiently by evaluating permanents.
