For the system in (8), we construct, based on 
, the
linear-product start system:
For every random choice of the coefficients, except for a set of measure
zero, the system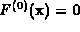 
will have seven finite regular
solutions. With every tuple of sets in (9)
there corresponds a linear system with a nonsingular matrix.
Of crucial importance is the observation that
solving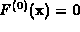 
corresponds to computing 
.
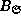Every monomial in the original system occurs also in a linear-product start system constructed from a supporting set structure, albeit with a different coefficient. In fact, set structures satisfying this property are defined to be supporting. Hereby we proved that by using a linear-product start system based on a supporting set structure we can obtain all isolated solutions.
