



Next: MVC: four lifting
Up: RoCo: root counting
Previous: Linear-product start systems
Many polynomial systems arising from practical applications have solution
sets that are invariant under permutations. This invariance can be read off
from the equations. The user can give the vector representations of the
generators of the symmetry group and a symmetric linear-product start system
might be constructed.
For the example in (8) we see that the system is invariant
under interchanging 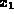 with
with 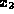 . If a set structure respects the
same symmetry relations, a symmetric linear-product system can be constructed.
It suffices to take in (10):
. If a set structure respects the
same symmetry relations, a symmetric linear-product system can be constructed.
It suffices to take in (10):
 , for i=1,2,3,4.
Because all systems in the homotopy have the same symmetry, only the generating
solution paths need to be traced. Moreover, we can restrict to fixed-point
space by setting
, for i=1,2,3,4.
Because all systems in the homotopy have the same symmetry, only the generating
solution paths need to be traced. Moreover, we can restrict to fixed-point
space by setting  , so that for this example only two solution paths
need to be followed, instead of seven.
, so that for this example only two solution paths
need to be followed, instead of seven.
Although the usefulness of this approach is illustrated by several
applications we have to be cautious about degeneracies.
Symmetry might prohibit the use of a linear-product start system, in the sense
that the formally constructed system does not qualify as a good start system
because there are not enough isolated solutions to start with.
Jan Verschelde
Thu Nov 21 10:50:01 MET 1996
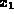 with
with 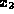 . If a set structure respects the
same symmetry relations, a symmetric linear-product system can be constructed.
It suffices to take in (10):
. If a set structure respects the
same symmetry relations, a symmetric linear-product system can be constructed.
It suffices to take in (10):
 , for i=1,2,3,4.
Because all systems in the homotopy have the same symmetry, only the generating
solution paths need to be traced. Moreover, we can restrict to fixed-point
space by setting
, for i=1,2,3,4.
Because all systems in the homotopy have the same symmetry, only the generating
solution paths need to be traced. Moreover, we can restrict to fixed-point
space by setting  , so that for this example only two solution paths
need to be followed, instead of seven.
, so that for this example only two solution paths
need to be followed, instead of seven.