



Next: Obtaining and Installing PHC
Up: PHCpack: a general-purpose solver
Previous: Putting it all together:
The progress on solving polynomial system has always been motivated by
the poor performance of the existing technology on practical examples.
To make the benchmarking more meaningful and relevant, most systems are
taken from practical applications, cited in the literature.
We refer to [Traverso 1993] and [Bini and Mourrain 1998] for similar collections.
In Tables 4 and 5 an overview of the
application database is given.
To save space, the algebraic description is omitted. Either
the reference or the PHC distribution file can be consulted.
Some systems appear in different guises, such as the cyclic n-roots
and the economics problem. It allows us to see how the particular
formulation of a problem can influence the solution process.
Some important characteristics of the systems are listed
in Tables 6 and 7.
Most systems arising from practical applications are deficient,
i.e.: have fewer roots than the root count.
The improvement of the mixed volume compared to the Bézout bounds is
in many cases really significant.
The black-box solver of PHC does not contain facilities to treat affine
roots properly,
therefore it may miss some isolated solutions with zero components.
The parameters of the black-box solver have been set to handle all
examples of the database.
In Tables 8 and 9 timings are listed
for a SPARCserver-1000.
We count 33 little examples, that require less than one minute to solve.
There are 38 larger examples, for which PHC needs between one minute and
an hour. Five big examples require more than one hour to solve.
Timings only have a temporary value. They are only good to measure
the difficulty of solving one system compared to another one.
The exponential gains from selecting a sharp root count are more important.
The black-box solver is certainly not the optimal way to solve a particular
system, although the timings give a good impression of the general
performance of the package.
Table 4:
An overview of the test database, part I.
Besides the name of the polynomial system, a reference to the literature
and a short description is mentioned.
| name |
reference |
title with description of the application |
| boon |
[Boon 1992] |
neurophysiology, posted by Sjirk Boon |
| butcher |
[Traverso 1993] |
Butcher's problem, from PoSSo test suite |
| butcher8 |
[Boege et al.1986] |
8-variable version of Butcher's problem |
| camera1s |
[Emiris 1997] |
camera displacement between 2 positions, frame 1 |
| caprasse |
[Traverso 1993] |
the system caprasse of the PoSSo test suite |
| cassou |
[Li et al. 1996] |
the system of Pierrette Cassou-Noguès |
| chemequ |
[Meintjes and Morgan 1990] |
chemical equilibrium of hydrocarbon combustion |
| cohn2 |
[Traverso 1993] |
the system cohn2 from the PoSSo test suite |
| cohn3 |
[Traverso 1993] |
the system cohn3 from the PoSSo test suite |
| comb3000 |
[Morgan 1987] |
Model A combustion chemistry example |
| conform1 |
[Emiris 1997] |
conformal analysis of cyclic molecules, instance 1 |
| cpdm5 |
[Gatermann 1990] |
5-dimensional system of Caprasse and Demaret |
| cyclic5 |
[Björk and Fröberg 1991] |
cyclic 5-roots problem |
| cyclic6 |
[Björk and Fröberg 1991] |
cyclic 6-roots problem |
| cyclic7 |
[Backelin and Fröberg 1991] |
cyclic 7-roots problem |
| cyclic8 |
[Björk and Fröberg 1994] |
cyclic 8-roots problem |
| d1 |
[Van Hentenryck et al. 1997] |
a sparse system, known as benchmark D1 |
| des18_3 |
[Nauheim 1998] |
a "dessin d'enfant", called des18_3 |
| des22_24 |
[Nauheim 1998] |
a "dessin d'enfant", called des22_24 |
| discret3s |
[Traverso 1993] |
system discret3, scaled by average coefficients |
| eco5 |
[Morgan 1987] |
5-dimensional economics problem |
| eco6 |
[Morgan 1987] |
6-dimensional economics problem |
| eco7 |
[Morgan 1987] |
7-dimensional economics problem |
| eco8 |
[Morgan 1987] |
8-dimensional economics problem |
| extcyc5 |
[Verschelde and Gatermann 1995] |
extended cyclic 5-roots to exploit symmetry |
| extcyc6 |
[Verschelde and Gatermann 1995] |
extended cyclic 6-roots to exploit symmetry |
| extcyc7 |
[Verschelde and Gatermann 1995] |
extended cyclic 7-roots to exploit symmetry |
| extcyc8 |
[Verschelde and Gatermann 1995] |
extended cyclic 8-roots to exploit symmetry |
| fourbar |
[Morgan and Wampler 1990] |
four-bar design problem, so-called 5-point problem |
| fbrfive4 |
[Wampler 1996] |
Four-bar linkage through 5 points, n=4 version |
| fbrfive12 |
[Wampler 1996] |
Four-bar linkage, coupler curve through 5 points |
| gaukwa2 |
[Stroud and Secrest 1966] |
Gaussian quadrature formula 2 knots, 2 weights |
| gaukwa3 |
[Stroud and Secrest 966] |
Gaussian quadrature formula 3 knots, 3 weights |
| gaukwa4 |
[Stroud and Secrest 1966] |
Gaussian quadrature formula 4 knots, 4 weights |
| geneig |
[Chu et al. 1988] |
generalized eigenvalue problem |
| heart |
[Nelsen and Hodgkin 1981] |
heart-dipole problem |
| i1 |
[Van Hentenryck et al. 1997] |
Benchmark i1 from Interval Arithmetic Benchmarks |
| ipp |
[Morgan and Sommese 1987b] |
six-revolute-joint problem of mechanics |
Table 6:
Characteristics of the polynomial systems, part I.
The dimension is n. D is the total degree of the system.
BZ is an m-homogeneous Bézout number, based on a partition
generated by a heuristic method.
BS is a generalized linear-product Bézout number,
based on a set structure generated by a heuristic method.
V is the mixed volume.
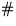 sols is number of isolated solutions found by PHC.
sols is number of isolated solutions found by PHC.
| name |
n |
D |
BZ |
BS |
V |
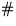 sols sols |
| boon |
6 |
1024 |
344 |
216 |
20 |
8 |
| butcher |
7 |
4608 |
2090 |
605 |
24 |
5 |
| butcher8 |
8 |
4608 |
1461 |
587 |
26 |
16 |
| camera1s |
6 |
64 |
20 |
20 |
20 |
20 |
| caprasse |
4 |
144 |
62 |
94 |
48 |
48 |
| cassou |
4 |
1344 |
368 |
361 |
24 |
16 |
| chemequ |
5 |
108 |
56 |
44 |
16 |
16 |
| cohn2 |
4 |
900 |
468 |
358 |
124 |
18 |
| cohn3 |
4 |
1080 |
484 |
358 |
213 |
102 |
| comb3000 |
10 |
96 |
66 |
28 |
16 |
16 |
| conform1 |
3 |
64 |
16 |
16 |
16 |
16 |
| cpdm5 |
5 |
243 |
243 |
243 |
242 |
157 |
| cyclic5 |
5 |
120 |
120 |
106 |
70 |
70 |
| cyclic6 |
6 |
720 |
720 |
588 |
156 |
156 |
| cyclic7 |
7 |
5040 |
5040 |
4200 |
924 |
924 |
| cyclic8 |
8 |
40320 |
40320 |
30365 |
2560 |
1152 |
| d1 |
12 |
4068 |
320 |
896 |
192 |
48 |
| des18_3 |
8 |
324 |
544 |
241 |
46 |
46 |
| des22_24 |
10 |
256 |
128 |
82 |
42 |
42 |
| discret3s |
8 |
256 |
128 |
128 |
128 |
128 |
| eco5 |
5 |
54 |
20 |
16 |
8 |
8 |
| eco6 |
6 |
162 |
48 |
36 |
16 |
16 |
| eco7 |
7 |
486 |
112 |
80 |
32 |
32 |
| eco8 |
8 |
1458 |
256 |
176 |
64 |
64 |
| extcyc5 |
5 |
120 |
120 |
106 |
70 |
70 |
| extcyc6 |
6 |
720 |
720 |
588 |
156 |
156 |
| extcyc7 |
7 |
5040 |
5040 |
4200 |
924 |
924 |
| extcyc8 |
8 |
40320 |
40320 |
30365 |
2560 |
1152 |
| fbrfive12 |
12 |
4096 |
96 |
96 |
36 |
36 |
| fbrfive4 |
4 |
256 |
96 |
194 |
36 |
36 |
| fourbar |
4 |
256 |
96 |
96 |
80 |
36 |
| gaukwa2 |
4 |
24 |
11 |
11 |
5 |
2 |
| gaukwa3 |
6 |
720 |
225 |
225 |
49 |
6 |
| gaukwa4 |
8 |
40320 |
6769 |
6769 |
729 |
24 |
| geneig |
6 |
243 |
10 |
10 |
10 |
10 |
| heart |
8 |
576 |
193 |
193 |
121 |
4 |
| i1 |
10 |
59049 |
452 |
437 |
66 |
66 |
| ipp |
8 |
256 |
96 |
96 |
64 |
48 |
Table 7:
Characteristics of the polynomial systems, part II.
The dimension is n. D is the total degree of the system.
BZ is an m-homogeneous Bézout number, based on a partition
generated by a heuristic method.
BS is a general linear-product Bézout number, based on a set structure
generated by a heuristic method. V is the mixed volume.
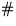 sols is number of isolated solutions found by PHC.
sols is number of isolated solutions found by PHC.
| name |
n |
D |
BZ |
BS |
V |
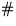 sols sols |
| ipp2 |
11 |
1024 |
576 |
848 |
288 |
16 |
| katsura5 |
6 |
32 |
32 |
32 |
32 |
32 |
| kin1 |
12 |
4608 |
320 |
896 |
192 |
48 |
| kinema |
9 |
64 |
240 |
64 |
64 |
40 |
| ku10 |
10 |
1024 |
2 |
2 |
2 |
2 |
| lorentz |
4 |
16 |
14 |
12 |
12 |
11 |
| lumped |
4 |
16 |
8 |
11 |
7 |
4 |
| mickey |
2 |
4 |
4 |
4 |
4 |
4 |
| noon3 |
3 |
27 |
29 |
21 |
21 |
21 |
| noon4 |
4 |
81 |
81 |
73 |
73 |
73 |
| noon5 |
5 |
243 |
243 |
233 |
233 |
233 |
| proddeco |
4 |
256 |
96 |
96 |
26 |
6 |
| puma |
8 |
128 |
16 |
32 |
16 |
16 |
| quadfor2 |
4 |
24 |
11 |
11 |
4 |
2 |
| quadgrid |
5 |
120 |
10 |
10 |
10 |
5 |
| rabmo |
9 |
36000 |
22740 |
7090 |
136 |
16 |
| rbpl |
6 |
486 |
160 |
160 |
160 |
150 |
| rbpl24 |
9 |
576 |
80 |
80 |
80 |
40 |
| redcyc5 |
4 |
24 |
24 |
19 |
14 |
14 |
| redcyc6 |
5 |
120 |
96 |
83 |
26 |
26 |
| redcyc7 |
6 |
720 |
720 |
511 |
132 |
132 |
| redcyc8 |
7 |
5040 |
3960 |
3107 |
320 |
144 |
| redeco5 |
5 |
8 |
12 |
8 |
8 |
8 |
| redeco6 |
6 |
16 |
28 |
16 |
16 |
16 |
| redeco7 |
7 |
32 |
64 |
32 |
32 |
32 |
| redeco8 |
8 |
64 |
144 |
64 |
64 |
64 |
| rediff3 |
3 |
8 |
8 |
8 |
7 |
7 |
| reimer5 |
5 |
720 |
720 |
720 |
720 |
144 |
| rose |
3 |
216 |
144 |
136 |
136 |
136 |
| s9_1 |
8 |
16 |
41 |
10 |
10 |
10 |
| sendra |
2 |
49 |
49 |
46 |
46 |
46 |
| solotarev |
4 |
36 |
10 |
8 |
6 |
6 |
| sparse5 |
5 |
100000 |
3840 |
3840 |
160 |
160 |
| speer |
4 |
625 |
384 |
246 |
96 |
43 |
| trinks |
6 |
24 |
24 |
18 |
10 |
10 |
| virasoro |
8 |
256 |
3072 |
256 |
200 |
200 |
| wood |
4 |
36 |
25 |
16 |
9 |
9 |
| wright |
5 |
32 |
32 |
32 |
32 |
32 |
Table 8:
Part I of timing summary on SPARCserver-1000,
with the black-box version made with the gnu-ada compiler.
The CPU time of the process is expressed in
hours, minutes, seconds, and milliseconds.
| name |
root counts |
|
|
|
start system |
|
|
|
continuation |
|
|
|
total time |
|
|
|
| boon |
0h |
0m |
0s |
190 |
0h |
0m |
5s |
868 |
0h |
0m |
14s |
394 |
0h |
0m |
20s |
937 |
| butcher |
0h |
0m |
13s |
267 |
0h |
0m |
29s |
23 |
0h |
1m |
44s |
962 |
0h |
2m |
28s |
449 |
| butcher8 |
0h |
0m |
50s |
513 |
0h |
0m |
25s |
188 |
0h |
4m |
20s |
602 |
0h |
5m |
38s |
507 |
| camera1s |
0h |
0m |
8s |
258 |
0h |
0m |
0s |
110 |
0h |
0m |
34s |
406 |
0h |
0m |
44s |
682 |
| caprasse |
0h |
0m |
0s |
769 |
0h |
0m |
10s |
4 |
0h |
0m |
17s |
80 |
0h |
0m |
28s |
888 |
| cassou |
0h |
0m |
1s |
145 |
0h |
0m |
10s |
688 |
0h |
1m |
3s |
439 |
0h |
1m |
15s |
972 |
| chemequ |
0h |
0m |
1s |
116 |
0h |
0m |
4s |
827 |
0h |
0m |
6s |
886 |
0h |
0m |
13s |
378 |
| cohn2 |
0h |
0m |
3s |
989 |
0h |
0m |
49s |
953 |
0h |
2m |
49s |
74 |
0h |
3m |
46s |
619 |
| cohn3 |
0h |
0m |
4s |
991 |
0h |
1m |
12s |
618 |
0h |
16m |
15s |
864 |
0h |
17m |
37s |
282 |
| comb3000 |
0h |
0m |
7s |
814 |
0h |
0m |
5s |
630 |
0h |
0m |
18s |
162 |
0h |
0m |
33s |
118 |
| conform1 |
0h |
0m |
0s |
42 |
0h |
0m |
0s |
45 |
0h |
0m |
3s |
880 |
0h |
0m |
4s |
310 |
| cpdm5 |
0h |
0m |
18s |
683 |
0h |
2m |
27s |
225 |
0h |
9m |
51s |
598 |
0h |
12m |
43s |
370 |
| cyclic5 |
0h |
0m |
0s |
562 |
0h |
0m |
11s |
768 |
0h |
0m |
32s |
469 |
0h |
0m |
45s |
993 |
| cyclic6 |
0h |
0m |
6s |
40 |
0h |
1m |
15s |
816 |
0h |
2m |
44s |
292 |
0h |
4m |
9s |
434 |
| cyclic7 |
0h |
1m |
15s |
74 |
0h |
15m |
49s |
391 |
0h |
27m |
50s |
521 |
0h |
45m |
21s |
434 |
| cyclic8 |
0h |
14m |
41s |
38 |
1h |
25m |
14s |
851 |
2h |
54m |
28s |
884 |
4h |
35m |
54s |
367 |
| d1 |
0h |
0m |
15s |
182 |
0h |
5m |
34s |
397 |
0h |
13m |
30s |
348 |
0h |
19m |
25s |
426 |
| des18_3 |
0h |
3m |
51s |
209 |
0h |
1m |
19s |
587 |
0h |
1m |
44s |
25 |
0h |
6m |
57s |
913 |
| des22_24 |
0h |
0m |
23s |
538 |
0h |
0m |
50s |
660 |
0h |
1m |
22s |
251 |
0h |
2m |
40s |
53 |
| discret3s |
0h |
2m |
20s |
4 |
0h |
0m |
0s |
719 |
0h |
56m |
20s |
922 |
0h |
58m |
52s |
121 |
| eco5 |
0h |
0m |
0s |
281 |
0h |
0m |
1s |
222 |
0h |
0m |
2s |
829 |
0h |
0m |
4s |
686 |
| eco6 |
0h |
0m |
2s |
217 |
0h |
0m |
4s |
132 |
0h |
0m |
6s |
771 |
0h |
0m |
13s |
785 |
| eco7 |
0h |
0m |
22s |
215 |
0h |
0m |
20s |
511 |
0h |
0m |
34s |
19 |
0h |
1m |
18s |
249 |
| eco8 |
0h |
5m |
28s |
66 |
0h |
1m |
1s |
471 |
0h |
1m |
55s |
472 |
0h |
8m |
27s |
528 |
| extcyc5 |
0h |
0m |
2s |
355 |
0h |
0m |
36s |
607 |
0h |
0m |
37s |
521 |
0h |
1m |
17s |
726 |
| extcyc6 |
0h |
0m |
30s |
15 |
0h |
1m |
45s |
137 |
0h |
2m |
56s |
572 |
0h |
5m |
15s |
706 |
| extcyc7 |
0h |
9m |
15s |
674 |
0h |
17m |
22s |
278 |
0h |
30m |
29s |
581 |
0h |
57m |
33s |
835 |
| extcyc8 |
1h |
58m |
58s |
816 |
1h |
36m |
57s |
179 |
3h |
58m |
54s |
943 |
7h |
36m |
30s |
580 |
| fbrfive12 |
0h |
1m |
30s |
161 |
0h |
1m |
6s |
686 |
0h |
2m |
18s |
859 |
0h |
4m |
58s |
570 |
| fbrfive4 |
0h |
0m |
0s |
463 |
0h |
0m |
17s |
283 |
0h |
1m |
2s |
690 |
0h |
1m |
21s |
972 |
| fourbar |
0h |
0m |
0s |
625 |
0h |
0m |
8s |
706 |
0h |
2m |
1s |
20 |
0h |
2m |
12s |
565 |
| gaukwa2 |
0h |
0m |
0s |
55 |
0h |
0m |
0s |
705 |
0h |
0m |
1s |
460 |
0h |
0m |
2s |
391 |
| gaukwa3 |
0h |
0m |
1s |
430 |
0h |
0m |
22s |
803 |
0h |
0m |
52s |
615 |
0h |
1m |
17s |
674 |
| gaukwa4 |
0h |
1m |
18s |
940 |
0h |
27m |
42s |
595 |
0h |
52m |
30s |
671 |
1h |
21m |
42s |
787 |
| geneig |
0h |
0m |
0s |
476 |
0h |
0m |
0s |
303 |
0h |
0m |
11s |
314 |
0h |
0m |
14s |
648 |
| heart |
0h |
1m |
10s |
899 |
0h |
3m |
14s |
236 |
0h |
4m |
39s |
75 |
0h |
9m |
6s |
712 |
| i1 |
0h |
0m |
37s |
869 |
0h |
0m |
49s |
215 |
0h |
1m |
59s |
959 |
0h |
3m |
29s |
913 |
| ipp |
0h |
1m |
4s |
541 |
0h |
1m |
21s |
14 |
0h |
1m |
47s |
940 |
0h |
4m |
16s |
287 |
Table 9:
Part II of timing summary on SPARCserver-1000,
with the black-box version made with the gnu-ada compiler.
The CPU time of the process is expressed in
hours, minutes, seconds, and milliseconds.
| name |
root counts |
|
|
|
start system |
|
|
|
continuation |
|
|
|
total time |
|
|
|
| ipp2 |
0h |
8m |
21s |
346 |
0h |
11m |
59s |
944 |
0h |
27m |
18s |
539 |
0h |
47m |
48s |
632 |
| katsura5 |
0h |
0m |
12s |
382 |
0h |
0m |
0s |
8 |
0h |
0m |
27s |
511 |
0h |
0m |
41s |
303 |
| kin1 |
0h |
2m |
2s |
926 |
0h |
5m |
39s |
399 |
0h |
11m |
37s |
403 |
0h |
19m |
25s |
259 |
| kinema |
0h |
2m |
28s |
847 |
0h |
0m |
0s |
22 |
0h |
3m |
11s |
205 |
0h |
5m |
42s |
168 |
| ku10 |
0h |
0m |
1s |
547 |
0h |
0m |
2s |
253 |
0h |
0m |
3s |
611 |
0h |
0m |
8s |
357 |
| lorentz |
0h |
0m |
0s |
173 |
0h |
0m |
0s |
23 |
0h |
0m |
6s |
633 |
0h |
0m |
7s |
256 |
| lumped |
0h |
0m |
0s |
289 |
0h |
0m |
0s |
714 |
0h |
0m |
1s |
975 |
0h |
0m |
3s |
255 |
| mickey |
0h |
0m |
0s |
8 |
0h |
0m |
0s |
2 |
0h |
0m |
0s |
175 |
0h |
0m |
0s |
248 |
| noon3 |
0h |
0m |
0s |
58 |
0h |
0m |
0s |
33 |
0h |
0m |
4s |
639 |
0h |
0m |
5s |
154 |
| noon4 |
0h |
0m |
0s |
399 |
0h |
0m |
0s |
103 |
0h |
0m |
51s |
160 |
0h |
0m |
53s |
163 |
| noon5 |
0h |
0m |
2s |
922 |
0h |
0m |
0s |
316 |
0h |
7m |
9s |
741 |
0h |
7m |
17s |
834 |
| proddeco |
0h |
0m |
0s |
299 |
0h |
0m |
10s |
135 |
0h |
0m |
42s |
488 |
0h |
0m |
54s |
26 |
| puma |
0h |
0m |
2s |
457 |
0h |
0m |
0s |
420 |
0h |
0m |
34s |
43 |
0h |
0m |
40s |
105 |
| quadfor2 |
0h |
0m |
0s |
24 |
0h |
0m |
0s |
183 |
0h |
0m |
0s |
910 |
0h |
0m |
1s |
271 |
| quadgrid |
0h |
0m |
4s |
451 |
0h |
0m |
0s |
159 |
0h |
0m |
14s |
627 |
0h |
0m |
20s |
443 |
| rabmo |
0h |
1m |
10s |
899 |
0h |
3m |
14s |
236 |
0h |
4m |
39s |
75 |
0h |
9m |
6s |
712 |
| rbpl |
0h |
1m |
32s |
693 |
0h |
0m |
0s |
670 |
0h |
10m |
24s |
859 |
0h |
12m |
4s |
957 |
| rbpl24 |
3h |
19m |
40s |
323 |
0h |
0m |
1s |
331 |
0h |
9m |
55s |
836 |
3h |
29m |
47s |
764 |
| redcyc5 |
0h |
0m |
0s |
348 |
0h |
0m |
2s |
767 |
0h |
0m |
3s |
505 |
0h |
0m |
6s |
995 |
| redcyc6 |
0h |
0m |
3s |
559 |
0h |
0m |
9s |
911 |
0h |
0m |
17s |
549 |
0h |
0m |
31s |
863 |
| redcyc7 |
0h |
0m |
54s |
118 |
0h |
1m |
56s |
885 |
0h |
3m |
12s |
794 |
0h |
6m |
7s |
216 |
| redcyc8 |
0h |
9m |
58s |
283 |
0h |
10m |
54s |
911 |
0h |
18m |
11s |
414 |
0h |
39m |
14s |
893 |
| redeco5 |
0h |
0m |
0s |
290 |
0h |
0m |
0s |
3 |
0h |
0m |
3s |
109 |
0h |
0m |
3s |
671 |
| redeco6 |
0h |
0m |
2s |
389 |
0h |
0m |
0s |
6 |
0h |
0m |
7s |
958 |
0h |
0m |
10s |
860 |
| redeco7 |
0h |
0m |
22s |
751 |
0h |
0m |
0s |
10 |
0h |
0m |
24s |
990 |
0h |
0m |
48s |
725 |
| redeco8 |
0h |
4m |
30s |
648 |
0h |
0m |
0s |
18 |
0h |
1m |
20s |
991 |
0h |
5m |
53s |
618 |
| rediff3 |
0h |
0m |
0s |
28 |
0h |
0m |
0s |
225 |
0h |
0m |
0s |
568 |
0h |
0m |
1s |
2 |
| reimer5 |
0h |
0m |
0s |
913 |
0h |
0m |
0s |
65 |
0h |
9m |
20s |
820 |
0h |
9m |
30s |
537 |
| rose |
0h |
0m |
0s |
86 |
0h |
0m |
0s |
347 |
0h |
2m |
26s |
320 |
0h |
2m |
30s |
262 |
| s9_1 |
0h |
0m |
0s |
663 |
0h |
0m |
0s |
65 |
0h |
0m |
14s |
843 |
0h |
0m |
17s |
344 |
| sendra |
0h |
0m |
0s |
50 |
0h |
0m |
0s |
131 |
0h |
0m |
18s |
328 |
0h |
0m |
19s |
474 |
| solotarev |
0h |
0m |
0s |
79 |
0h |
0m |
0s |
365 |
0h |
0m |
1s |
37 |
0h |
0m |
1s |
695 |
| sparse5 |
0h |
0m |
0s |
396 |
0h |
0m |
21s |
672 |
0h |
3m |
45s |
456 |
0h |
4m |
11s |
36 |
| speer |
0h |
0m |
1s |
554 |
0h |
0m |
52s |
9 |
0h |
13m |
35s |
109 |
0h |
14m |
31s |
786 |
| trinks |
0h |
0m |
0s |
666 |
0h |
0m |
1s |
855 |
0h |
0m |
5s |
962 |
0h |
0m |
8s |
967 |
| virasoro |
3h |
40m |
50s |
731 |
0h |
7m |
0s |
273 |
0h |
7m |
42s |
993 |
3h |
55m |
41s |
856 |
| wood |
0h |
0m |
0s |
55 |
0h |
0m |
0s |
761 |
0h |
0m |
2s |
860 |
0h |
0m |
3s |
912 |
| wright |
0h |
0m |
1s |
332 |
0h |
0m |
0s |
6 |
0h |
0m |
13s |
251 |
0h |
0m |
15s |
210 |
The demonstration database of polynomial systems is still growing in
order to increase the awareness of the importance and relevance of
solving polynomial systems to applied mathematics and scientific computing.
In closing some user applications of PHC are mentioned.
PHC was used actively by Charles Wampler
[1996] to count
the roots of various systems in mechanical design.
Frank Sottile applied PHC to compute root counts for linear subspace
intersections of the Schubert calculus, see [Sottile 1998] for various tables.
A third example comes from computer graphics.
To show that the 12 lines tangent to four given spheres can all be real,
Thorsten Theobald used PHC, choosing appropriate parameters in the algebraic
formulation set up by Cassiano Durand.




Next: Obtaining and Installing PHC
Up: PHCpack: a general-purpose solver
Previous: Putting it all together:
Jan Verschelde
3/7/1999