Lecture 26: Plotting in Three Dimensions and Beyond

The default installation of SageMath may not come with the Java code (Jmol) needed to manipulate graphics objects. A work around (is needed on Windows computers) is to use tachyon as the viewer. In particular, if p is the result of a plotting command, render the plot p as

show(p, viewer='tachyon')

Of course, as always, the SageMath Cell Server and CoCalc are equally valid alternatives.

In three dimensions, we distinguish between surfaces and space curves. A surface may be given in three different ways. Which command to use depends on the definition of the surface.

1. Given as a function \(z = f(x, y)\), use plot3d.

2. Implicitly as an equation \(f(x,y,z) = 0\), use implicit_plot3d.

3. In parameter form as \((x(s,t), y(s,t), z(s,t))\), use parametric_plot3d.

Space curves may be given in two different ways. Which command to use depends on the definition of the space curve.

1. In parameter form as \((x(t), y(t), z(t)\), use parametric_plot3d.

2. Implicitly, as the intersection of two equations \(f(x,y,z) = 0\) and \(g(x,y,z) = 0\), use implicit_plot3d twice.

Observe there are no special commands for space curves, the parametric_plot3d and implicit_plot3d are used differently.

Surface Plots

A surface can be defined as \(z = f(x,y)\), where for each point in the plane with coordinates \((x,y)\) the corresponding height \(z\) is defined by an expression or function in \(x\) and \(y\). In this case we use plot3d. For example, to plot the surface defined by \(z = \cos(x y)\), for \((x,y) \in [-\pi, +\pi] \times [-\pi, +\pi]\) we do:

x, y = var('x,y')
plot3d(cos(x*y), (x, -pi, pi), (y, -pi, pi))

The plot is shown in Fig. 41.

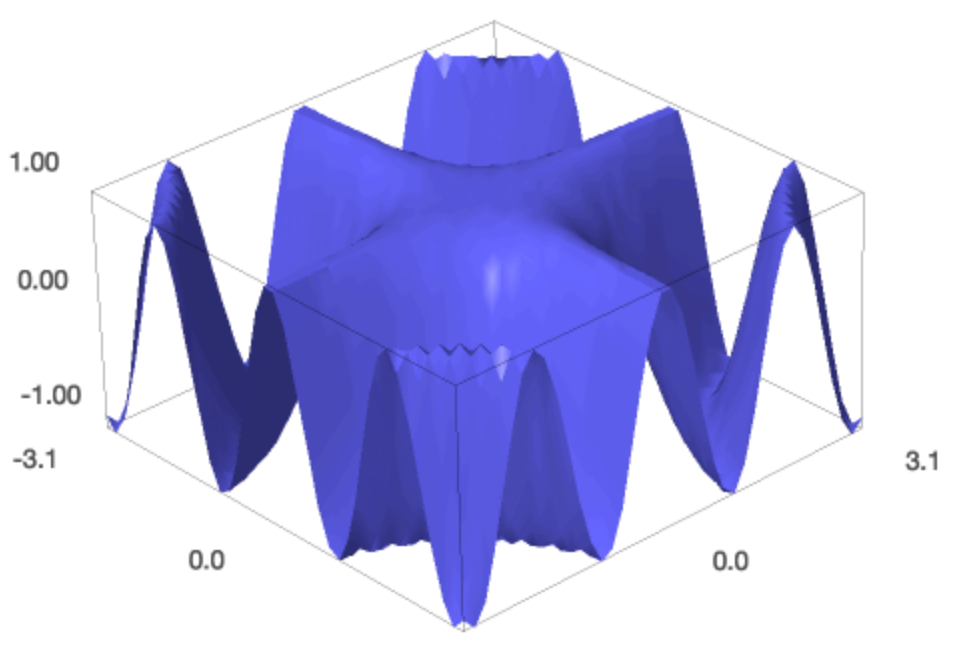
Fig. 41 The plot of the surface \(z = \cos(x y)\).

We observe that the plot is rather flat and this is because the values for \(x\) and \(y\) range from \(-3.14\) to \(+3.14\), where as the \(\cos(\cdot)\) takes values between \(-1\) and \(+1\). To make the plot less flat, we change the aspect_ratio and we make the plot spin, as follows:

plot3d(cos(x*y), (x, -pi, pi), (y, -pi, pi), \
    aspect_ratio=(1,1,2), spin=1)

We can change the viewing angle with the methods rotateX() and rotateZ() for example.

plot3d(cos(x*y), (x, -pi, pi), (y, -pi, pi), \
    aspect_ratio=(1,1,2)).rotateX(pi/2).rotateZ(pi/4)

The result of the rotation of the viewing angles is shown in Fig. 42.

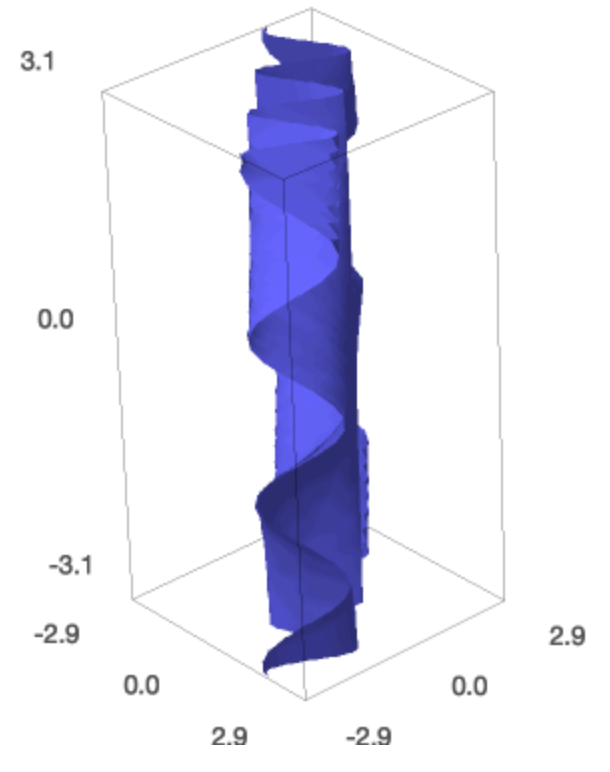
Fig. 42 The plot of the surface \(z = \cos(x y)\) with adjusted viewing angles.

By default, the value for opacity is 1, we can make the plot more transparant by lowering that value. We can also increase the number of plot points.

plot3d(cos(x*y), (x, -pi, pi), (y, -pi, pi), aspect_ratio=(1,1,2), \
    plot_points=[60,60], opacity=0.75).rotateX(pi/10).rotateY(-pi/10)

See Fig. 43 for the corresponding picture.

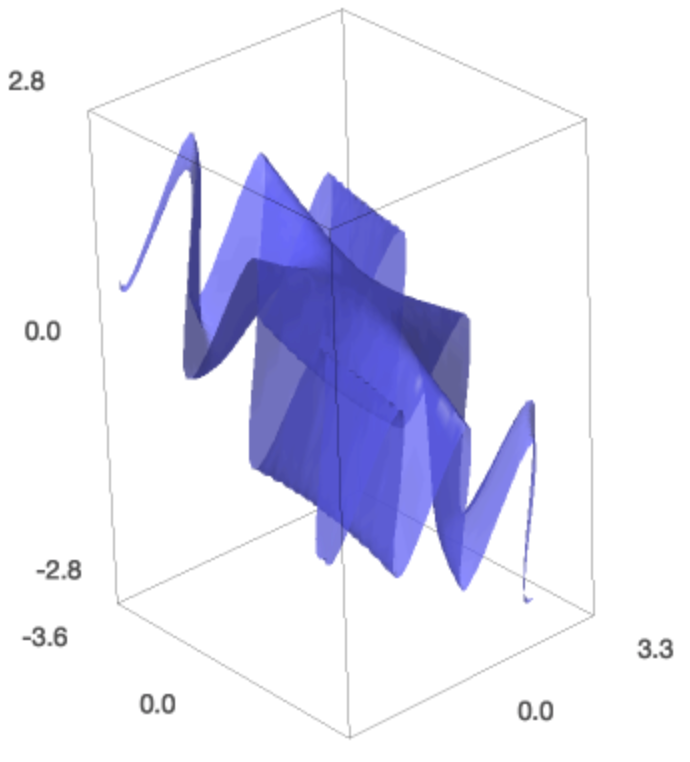
Fig. 43 The plot of the surface \(z = \cos(x y)\) with adjusted viewing angles, defined number of plot points, and an opacity factor.

Instead of trying to guess the best number of plot points, we can set adaptive to True. Setting color to 'automatic' chooses a rainbow of colors, we can set the number of colors with num_colors.

plot3d(cos(x*y), (x, -pi, pi), (y, -pi, pi), adaptive=True, \
    aspect_ratio=(1,1,2), color='automatic', num_colors=256)

The colorful plot is shown in Fig. 44.

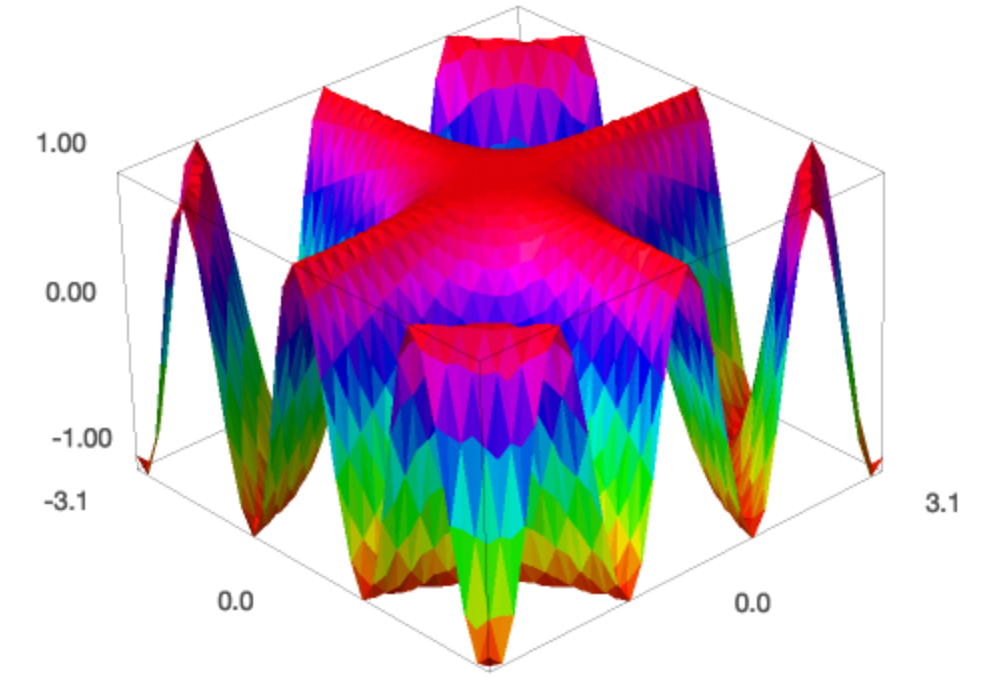
Fig. 44 The plot of the surface \(z = \cos(x y)\) with an adaptive choice of plot points and with many colors.

Surfaces may be given in parametric form by three expressions in two variables, say \(u\) and \(v\), as \(x = f_x(u,v), y = f_y(u,v)\), and \(z = f_z(u,v)\). Then we use parametric_plot3d. The example below comes from the SageMath documentation.

u, v = var('u, v')
fx = cos(u)*(4*sqrt(1-v^2)*sin(abs(u))^abs(u))
fy = sin(u) *(4*sqrt(1-v^2)*sin(abs(u))^abs(u))
fz = v
heart = parametric_plot3d([fx, fy, fz], (u, -pi, pi), (v, -1, 1), \
    color='red').rotateX(-pi/9).rotateY(-pi/2).rotateZ(pi/4)
show(heart, frame=False)

Observe how we can prevent the bounding box from appearing. The surface is shown in Fig. 45.

Fig. 45 The plot of a parametric surface.

Space Curves

A space curve is defined by a parametric plot of 3 functions in one variable. For example, the twisted cubic is defined by \(x = t, y = t^2, z = t^3\).

t = var('t')
twisted = (t, t^2, t^3)
parametric_plot3d(twisted, (t, -1, 1))

We can make the curve look red and thicker.

pt = parametric_plot3d(twisted, (t, -1, 1), color='red', thickness=5)
show(pt)

The result of the parametric_plot3d is shown in Fig. 46.

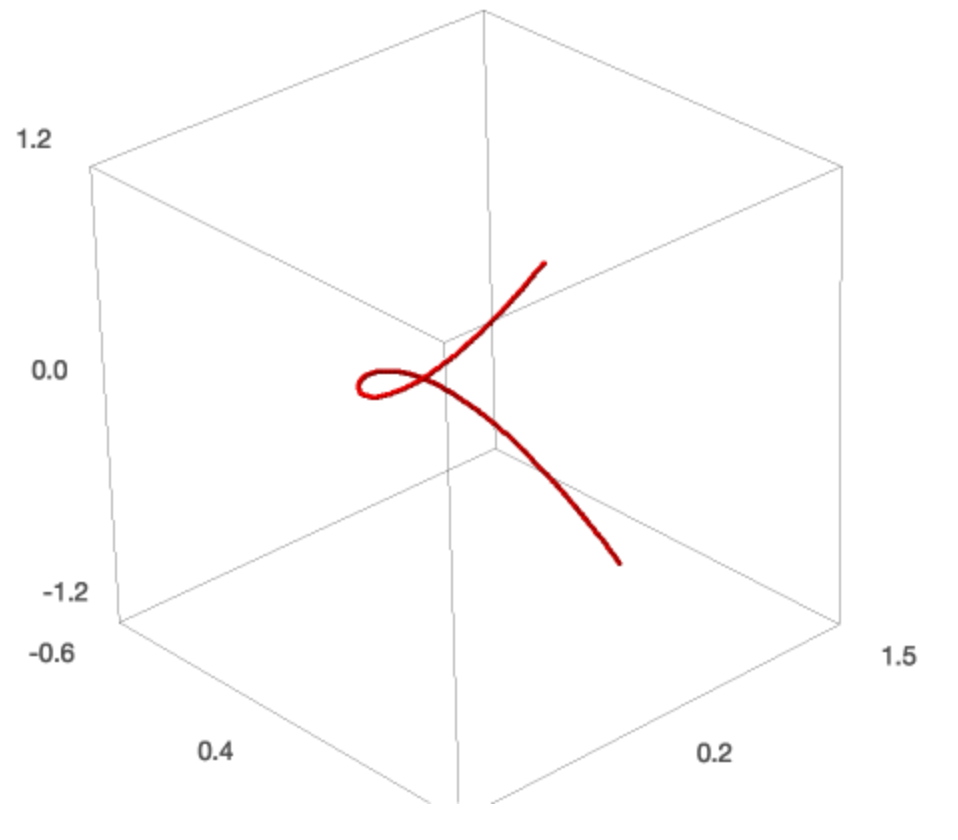
Fig. 46 A plot of the space curve \((t, t^2, t^3)\), the twisted cubic.

There is a bounding box attribute associated to the plot.

pt.bounding_box()

We need to know the bounding box if we want to add to the plot, so we know which ranges for the three coordinates to choose. The twisted cubic is the intersection of a parabolic and a cubic cylinder. The parabolic cylinder has its base in the \((x,y)\)-plane and from the parametric representation of the twisted cubic \((x=t, y=t^2)\), we can derive the implicit equation as \(x^2 - y = 0\).

x, y, z = var('x,y,z')
c2 = implicit_plot3d(x^2 - y,(x,-1,1),(y,0,1), (z,-1,1))
show(pt+c2)

The result of the implicit_plot3d is shown in Fig. 47.

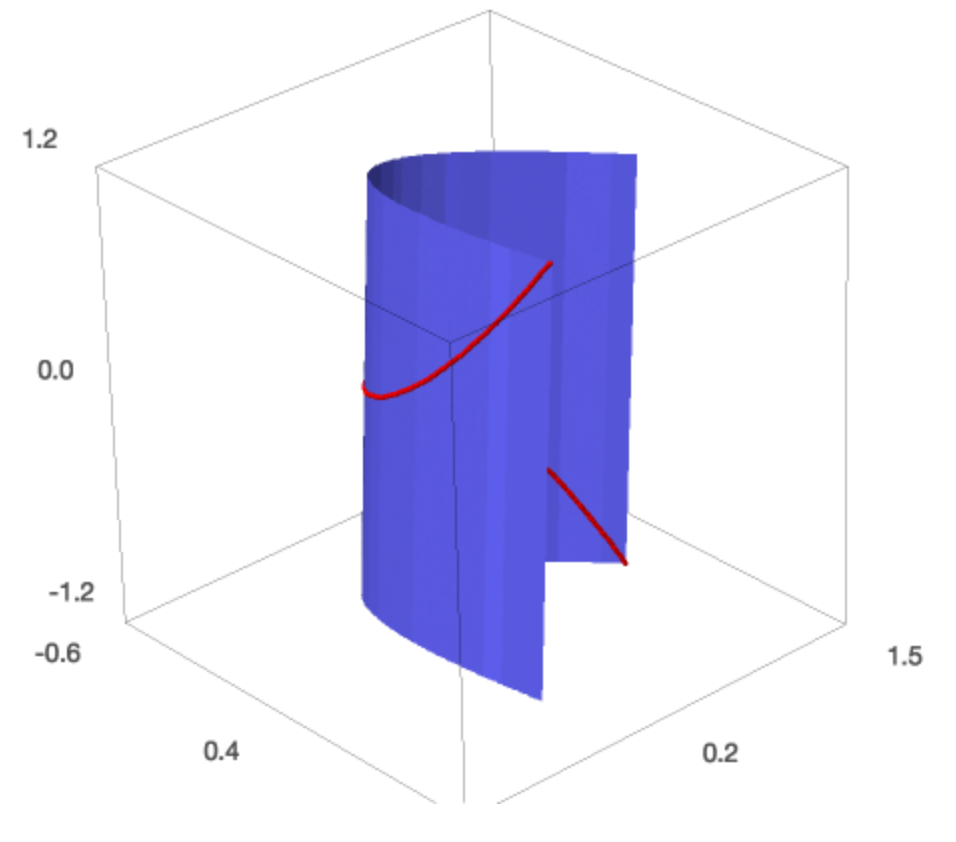
Fig. 47 The twisted cubic \((t, t^2, t^3)\) on the parabolic cylinder \(x^2 - y = 0\).

The cubic cylinder has its base in the \((x, z)\)-plane and its equation can be derived from the parameter representation for the twisted cubic, \((x=t, z=t^3)\) so the equation is \(x^3 - z = 0\).

c3 = implicit_plot3d(x^3 - z,(x,-1,1),(y,0,1), (z,-1,1), color='green')
show(pt+c2+c3)

We then see the two cylinders with the twisted cubic as their intersection.

Four Dimensional Plots with Colormaps

With colormaps we can plot in four dimensions. Let us first explore the use of colormaps. We can color surfaces with a colormap. As an example we take the Moebius strip. First we plot it without color.

from sage.plot.plot3d.parametric_surface import MoebiusStrip
ms = MoebiusStrip(3,1,plot_points=200).rotateX(-pi/8)
show(ms)

The figure is shown in Fig. 48.

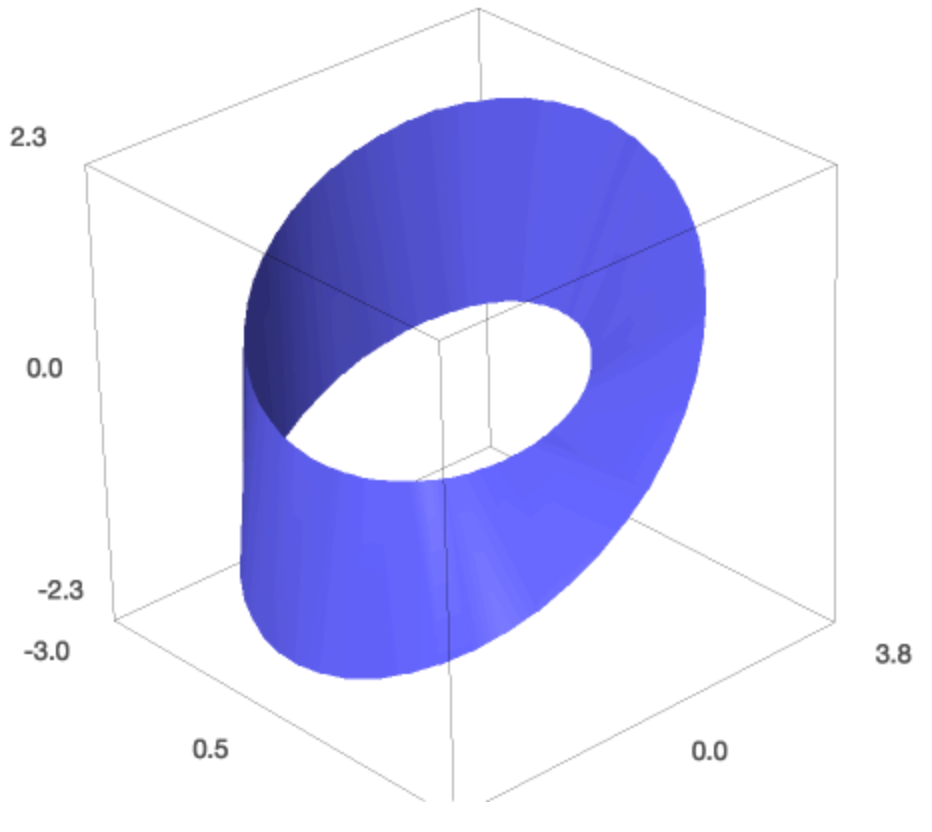
Fig. 48 The Moebius strip is a one-sided surface.

Now we apply a colormap.

cm = colormaps.ocean
def c(x,y): return sin(x*y)**2
mscm = MoebiusStrip(3,1,plot_points=200,color=(c,cm)).rotateX(-pi/8)
show(mscm, frame=False, viewer='tachyon')

The Moebius strip shown in colors is displayed in Fig. 49.

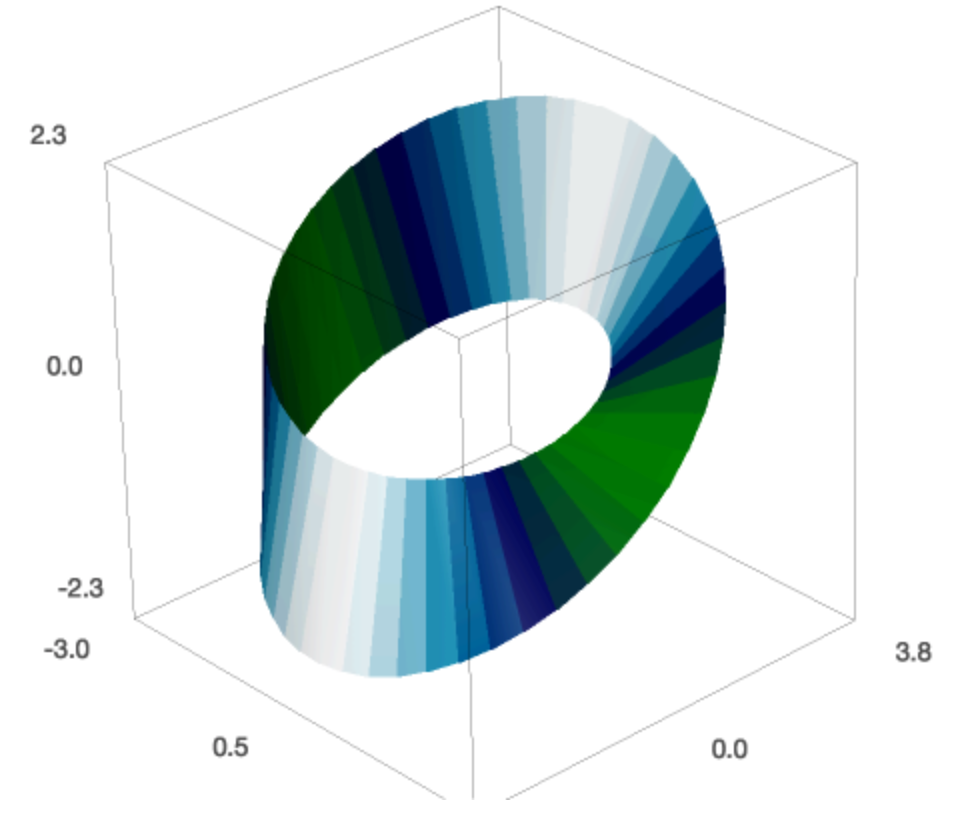
Fig. 49 A colored one sided surface, the Moebius strip.

We can use colormaps to make four dimensional plots. Consider the cubic root of a complex number.

u, v = var('u,v')
w = u + I*v
z = w^3
x = real_part(z)
y = imag_part(z)

We consider any complex number w. Because u and v are real numbers, so we can simplify their real and imaginary parts.

D = {real_part(u):u, imag_part(u):0, real_part(v):v, imag_part(v):0}
xx = x.subs(D)
yy = y.subs(D)
print(xx)
print(yy)

and then we see u^3 - 3*u*v^2 and 3*u^2*v - v^3 as the expressions for xx and yy. We can now plot the surface using the expressions for xx and yy as functions of u and v, just as parametric_plot3d((xx, yy, u), (u, -1, 1), (v, -1, 1)).

Why does this represent the cubic root? Well, the height of the surface is u, the real part of the complex number w we started with. The xx and yy are the real and imaginary parts of the z, where z was obtained by taking the number u + I*v to the third power.

Going to polar coordinates produces a nicer plot.

r, t = var('r,t')
rt = {u:r*cos(t), v:r*sin(t)}
px = xx.subs(rt)
py = yy.subs(rt)

and now we make the plot as

parametric_plot3d((px, py, r*cos(t)), (r, 0, 1), (t, 0, 2*pi), adaptive=True)

The plot is shown in Fig. 50.

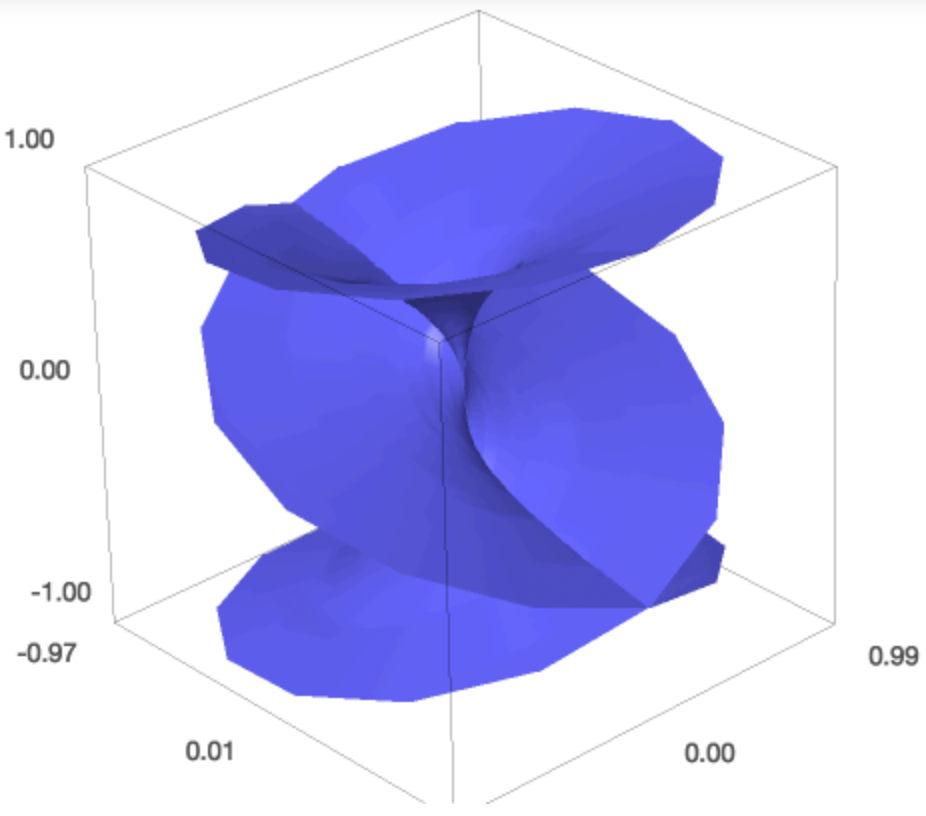
Fig. 50 A plot of the real part of the cubic root surface.

Now we would like as color to use the imaginary part, v = r*sin(t).

cm = colormaps.autumn
def c(r,t): return r*sin(t)
cr = parametric_plot3d((px, py, r*cos(t)), (r,0,1), (t, 0, 2*pi), \
    adaptive=True,color=(c,cm)).rotateX(pi/10).rotateY(-pi).rotateZ(pi/2)
show(cr, frame=False, viewer='tachyon')

and this produces the plot shown in Fig. 51.

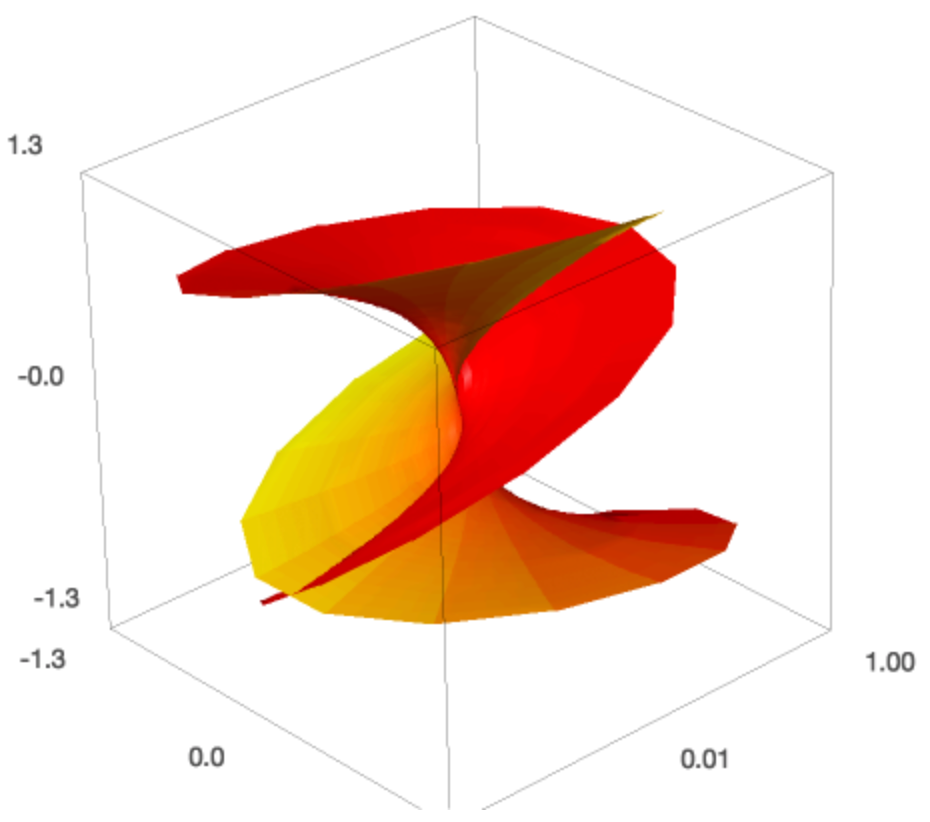
Fig. 51 The plot of a Riemann surface.

The height of the surface is the real part and the color of the surface represents the imaginary part of the cubic root. This is a four dimensional plot, also called a Riemann surface.

Assignments

1. Consider \(h = 2 \cos(0.4x) \cos(0.4y) + 5 x y e^{-(x^2 + y^2)} + 3 e^{-((x-2)^2 + (y-2)^2)}\). Choose appropriate ranges for \(x\) and \(y\) so that the plot of this surface shows three peaks.

2. The Viviani curve is a space curve defined by \(x = \cos^2(t)\), \(y = \cos(t) \sin(t)\), and \(z = \sin(t)\). Give the SageMath command to plot this space curve.

3. The Viviani curve is defined as the intersection of the sphere \(x^2 + y^2 + z^2 = 1\) and the cylinder \(x^2 + y^2 = 1\). Plot the two surfaces and emphasize their intersection adding the result of the plot of the previous exercise.

4. A torus knot is defined by \(r = 2 + 4/5 \cos(7t)\), \(x = r \cos(4 t)\), \(y = r \sin(4 t)\), and \(z = \sin(7t)\). Plot this knot with SageMath.

5. Consider the surface defined by the equation \(f(x,y,z) = x^3 - y^2 - z^2 = 0\).

   1. Give the SageMath command to plot this surface, for \(x \in [0, 1]\) and for \(y, z \in [-1, 1]\). What do you see at (0,0,0)? Describe.

   2. Replace \(z\) by zero and transform the curve defined by \(f(x, y, 0) = 0\) into polar coordinates. Write the SageMath command to graph the curve in polar coordinates. Use good bounds for the range of \(t\).