Device Memories and Matrix Multiplication¶

We take a closer look at different memories on the GPU and how it relates to the problem of matrix multiplication.

Device Memories¶

Before we launch a kernel, we have to allocate memory on the device, and to transfer data from the host to the device. By default, memory on the device is global memory. In addition to global memory, we distinguish between

registers for storing local variables,
shared memory for all threads in a block,
constant memory for all blocks on a grid.

The importance of understanding different memories is in the calculation of the expected performance level of kernel code.

the Compute to Global Memory Access (CGMA) ratio

The Compute to Global Memory Access (CGMA) ratio is the number of floating-point calculations performed for each access to the global memory within a region of a CUDA program.

If the CGMA ratio is 1.0, then the memory clock rate determines the upper limit for the performance. While memory bandwidth on a GPU is superior to that of a CPU, we will miss the theoretical peak performance by a factor of ten.

The different types of memory are schematically presented in Fig. 92.

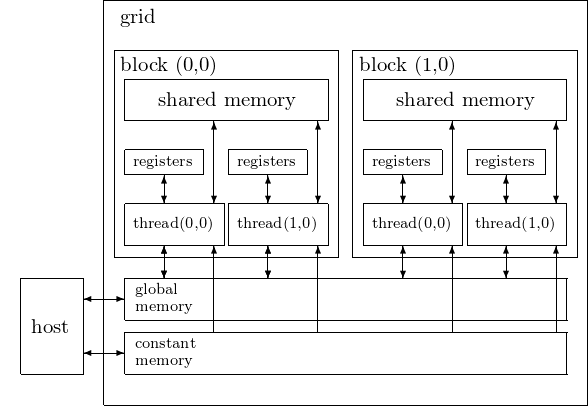
Fig. 92 The CUDA device memory types.

Registers are allocated to individual threads. Each thread can access only its own registers. A kernel function typically uses registers to hold frequently accessed variables that are private to each thread.

Number of 32-bit registers available per block:

8,192 on the GeForce 9400M,
32,768 on the Tesla C2050/C2070,
65,536 on the Tesla K20C and the P100.

A typical CUDA kernel may launch thousands of threads. However, having too many local variables in a kernel function may prevent all blocks from running in parallel.

Like registers, shared memory is an on-chip memory. Variables residing in registers and shared memory can be accessed at very high speed in a highly parallel manner. Unlike registers, which are private to each thread, all threads in the same block have access to shared memory.

Amount of shared memory per block:

16,384 byes on the GeForce 9400M,
49,152 bytes on the Tesla C2050/C2070,
49,152 bytes on the Tesla K20c and the P100.

The constant memory supports short-latency, high-bandwidth, read-only access by the device when all threads simultaneously access the same location.

The GeForce 9400M has 65,536 bytes of constant memory, the total amount of global memory is 254 MBytes.
The Tesla C2050/C2070 has 65,536 bytes of constant memory, the total amount of global memory is 2,687 MBytes, with 786,432 bytes of L2 cache.
The Tesla K20c has 65,536 bytes of constant memory, the total amount of global memory is 4,800 MBytes with 1,310,720 bytes of L2 cache.
The Tesla P100 has 65,536 bytes of constant memory, the total amount of global memory is 16,276 MBytes with 4,194,304 bytes of L2 cache.

The relationshiop between thread organization and different types of device memories is shown in Fig. 93, copied from the NVIDIA Whitepaper on Kepler GK110.

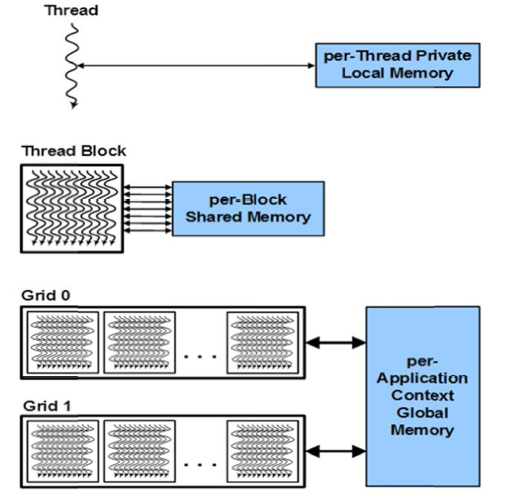
Fig. 93 Registers, shared, and global memory per thread, thread block, and grid.

Each variable is stored in a particular type of memory, has a scope and a lifetime.

Scope is the range of threads that can access the variable. If the scope of a variable is a single thread, then a private version of that variable exists for every single thread. Each thread can access only its private version of the variable.

Lifetime specifies the portion of the duration of the program execution when the variable is available for use. If a variable is declared in the kernel function body, then that variable is available for use only by the code of the kernel. If the kernel is invoked several times, then the contents of that variable will not be maintained across these invocations.

We distinguish between five different variable declarations, based on their memory location, scope, and lifetime, summarized in Table 27.

Table 27 CUDA variable declarations.¶
variable declaration	memory	scope	lifetime
atomic variables	register	thread	kernel
array variables	local	thread	kernel
`__device__.__shared__.int v`	shared	block	kernel
`__device__.int v`	global	grid	program
`__device__.__constant__.int v`	constant	grid	program

The __device__ in front of __shared__ is optional.

Matrix Multiplication¶

In an application of tiling, let us examine the CGMA ratio. In our simple implementation of the matrix-matrix multiplication \(C = A \cdot B\), we have the statement

C[i] += (*(pA++))*(*pB);

where

C is a float array; and
pA and pB are pointers to elements in a float array.

For the statement above, the CGMA ratio is 2/3:

for one addition and one multiplication,
we have three memory accesses.

To improve the CGMA ratio, we apply tiling. For \(A \in {\mathbb R}^{n \times m}\) and \(B \in {\mathbb R}^{m \times p}\), the product \(C = A \cdot B \in {\mathbb R}^{n \times p}\). Assume that \(n\), \(m\), and \(p\) are multiples of some \(w\), e.g.: \(w = 8\). We compute \(C\) in tiles of size \(w \times w\):

Every block computes one tile of \(C\).
All threads in one block operate on submatrices:

\[C_{i,j} = \sum_{k=1}^{m/w} A_{i,k} \cdot B_{k,j}.\]
The submatrices \(A_{i,k}\) and \(B_{k,j}\) are loaded from global memory into shared memory of the block.

The tiling of matrix multiplication as it relates to shared memory is shown in Fig. 94.

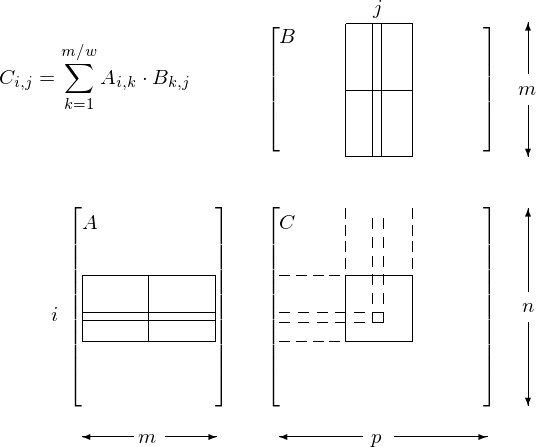
Fig. 94 Tiled matrix multiplication and shared memory.

The GPU computing SDK contains as one of the examples matrixMul and this matrixMul is explained in great detail in the CUDA programming guide. We run it on the GeForce 9400M, the Tesla C2050/C2070, and the Tesla K20C.

A session on the GeForce 9400M is below:

/Developer/GPU Computing/C/bin/darwin/release $ ./matrixMul
[matrixMul] starting...

[ matrixMul ]
./matrixMul
     Starting (CUDA and CUBLAS tests)...

Device 0: "GeForce 9400M" with Compute 1.1 capability

Using Matrix Sizes: A(160 x 320), B(160 x 320), C(160 x 320)

Runing Kernels...

> CUBLAS         7.2791 GFlop/s, Time = 0.00225 s, Size = 16384000 Ops

> CUDA matrixMul 5.4918 GFlop/s, Time = 0.00298 s, Size = 16384000 Ops,\
NumDevsUsed = 1, Workgroup = 256

Comparing GPU results with Host computation...

Comparing CUBLAS & Host results
CUBLAS compares OK

Comparing CUDA matrixMul & Host results
CUDA matrixMul compares OK

[matrixMul] test results...
PASSED

A session on the Tesla C2050/C2070 is below:

/usr/local/cuda/sdk/C/bin/linux/release jan$ ./matrixMul
[matrixMul] starting...
[ matrixMul ]
./matrixMul Starting (CUDA and CUBLAS tests)...

Device 0: "Tesla C2050 / C2070" with Compute 2.0 capability

Using Matrix Sizes: A(640 x 960), B(640 x 640), C(640 x 960)

Runing Kernels...

> CUBLAS         Throughput = 424.8840 GFlop/s, Time = 0.00185 s, \
Size = 786432000 Ops

> CUDA matrixMul Throughput = 186.7684 GFlop/s, Time = 0.00421 s, \
Size = 786432000 Ops, NumDevsUsed = 1, Workgroup = 1024

Comparing GPU results with Host computation...

Comparing CUBLAS & Host results
CUBLAS compares OK

Comparing CUDA matrixMul & Host results
CUDA matrixMul compares OK

[matrixMul] test results...
PASSED

A session on the K20C is below:

$ /usr/local/cuda/samples/0_Simple/matrixMul/matrixMul
[Matrix Multiply Using CUDA] - Starting...

GPU Device 0: "Tesla K20c" with compute capability 3.5

MatrixA(320,320), MatrixB(640,320)
Computing result using CUDA Kernel...
done
Performance= 246.13 GFlop/s, Time= 0.533 msec, Size= 131072000 Ops, \
WorkgroupSize= 1024 threads/block
Checking computed result for correctness: Result = PASS

Note: For peak performance, please refer to the matrixMulCUBLAS \
example.
$

The theoretical peak performance of the K20c is 1.17 TFlops double precision, and 3.52 TFlops single precision. The matrices that are multiplied have single float as type.

With CUBLAS we can go for peak performance:

$ /usr/local/cuda/samples/0_Simple/matrixMulCUBLAS/matrixMulCUBLAS
[Matrix Multiply CUBLAS] - Starting...
/usr/bin/nvidia-modprobe: unrecognized option: "-u"

GPU Device 0: "Tesla K20c" with compute capability 3.5

MatrixA(320,640), MatrixB(320,640), MatrixC(320,640)
Computing result using CUBLAS...done.
Performance= 1171.83 GFlop/s, Time= 0.112 msec, Size= 131072000 Ops
Computing result using host CPU...done.
Comparing CUBLAS Matrix Multiply with CPU results: PASS
$

The theoretical peak performance of the K20c is 1.17 TFlops double precision, and 3.52 TFlops single precision. The matrices that are multiplied have single float as type. The newer P100 has a theoretical peak performance (with GPU Boost) of 18.7 TFlops in half precision, 9.3 TFlops in single precision, and 4.7 TFlops in double precision. First we run the simple version of the matrix multiplication:

$ /usr/local/cuda/samples/0_Simple/matrixMul/matrixMul
[Matrix Multiply Using CUDA] - Starting...
GPU Device 0: "Tesla P100-PCIE-16GB" with compute capability 6.0

MatrixA(320,320), MatrixB(640,320)
Computing result using CUDA Kernel...
done
Performance= 1909.26 GFlop/s, Time= 0.069 msec, Size= 131072000 Ops,
WorkgroupSize= 1024 threads/block
Checking computed result for correctness: Result = PASS

NOTE: The CUDA Samples are not meant for performance measurements.
Results may vary when GPU Boost is enabled.
$

Then a run with CUBLAS on the P100:

$ /usr/local/cuda/samples/0_Simple/matrixMulCUBLAS/matrixMulCUBLAS
[Matrix Multiply CUBLAS] - Starting...
GPU Device 0: "Tesla P100-PCIE-16GB" with compute capability 6.0

MatrixA(640,480), MatrixB(480,320), MatrixC(640,320)
Computing result using CUBLAS...done.
Performance= 3089.82 GFlop/s, Time= 0.064 msec, Size= 196608000 Ops
Computing result using host CPU...done.
Comparing CUBLAS Matrix Multiply with CPU results: PASS

NOTE: The CUDA Samples are not meant for performance measurements.
Results may vary when GPU Boost is enabled.
$

A second run gave the following:

Performance= 3106.43 GFlop/s, Time= 0.063 msec, Size= 196608000 Ops

For single floats, the theoretical peak performance is 9.3 TFlops.

The code of the kernel of matrixMul is listed next.

template <int BLOCK_SIZE> __global__ void
matrixMul( float* C, float* A, float* B, int wA, int wB)
{
    int bx = blockIdx.x;   // Block index
    int by = blockIdx.y;
    int tx = threadIdx.x;  // Thread index
    int ty = threadIdx.y;
    // Index of the first sub-matrix of A processed by the block
    int aBegin = wA * BLOCK_SIZE * by;
    // Index of the last sub-matrix of A processed by the block
    int aEnd   = aBegin + wA - 1;
    // Step size used to iterate through the sub-matrices of A
    int aStep  = BLOCK_SIZE;
    // Index of the first sub-matrix of B processed by the block
    int bBegin = BLOCK_SIZE * bx;
    // Step size used to iterate through the sub-matrices of B
    int bStep  = BLOCK_SIZE * wB;
    // Csub is used to store the element of the block sub-matrix
    // that is computed by the thread
    float Csub = 0;

    // Loop over all the sub-matrices of A and B
    // required to compute the block sub-matrix
    for (int a = aBegin, b = bBegin;
             a <= aEnd;
             a += aStep, b += bStep) {

        // Declaration of the shared memory array As used to
        // store the sub-matrix of A
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];

        // Declaration of the shared memory array Bs used to
        // store the sub-matrix of B
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
        // Load the matrices from device memory
        // to shared memory; each thread loads
        // one element of each matrix
        AS(ty, tx) = A[a + wA * ty + tx];
        BS(ty, tx) = B[b + wB * ty + tx];

        // Synchronize to make sure the matrices are loaded
        __syncthreads();

        // Multiply the two matrices together;
        // each thread computes one element
        // of the block sub-matrix
#pragma unroll
        for (int k = 0; k < BLOCK_SIZE; ++k)
            Csub += AS(ty, k) * BS(k, tx);

        // Synchronize to make sure that the preceding
        // computation is done before loading two new
        // sub-matrices of A and B in the next iteration
        __syncthreads();
    }

    // Write the block sub-matrix to device memory;
    // each thread writes one element
    int c = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
    C[c + wB * ty + tx] = Csub;
}

The emphasis in this lecture is on (1) the use of device memories; and (2) data organization (tiling) and transfer. In the next lecture we will come back to this code, and cover thread scheduling (1) the use of blockIdx; and (2) thread synchronization.

Bibliography¶

Vasily Volkov and James W. Demmel: Benchmarking GPUs to tune dense linear algebra. In Proceedings of the 2008 ACM/IEEE conference on Supercomputing. IEEE Press, 2008. Article No. 31.

Exercises¶

Compile the matrixMul of the GPU Computing SDK on your laptop and desktop and run the program.
Consider the matrix multiplication code of last lecture and compute the CGMA ratio.
Adjust the code for matrix multiplication we discussed last time to use shared memory.

Device Memories and Matrix Multiplication¶

Device Memories¶

Matrix Multiplication¶

Bibliography¶

Exercises¶

Table Of Contents

Previous topic

Next topic

This Page