Thread Organization and Matrix Multiplication¶

In this lecture we look at the problem of multiplying two matrices, from the perspective of the thread organization.

Thread Organization¶

The code that runs on the GPU is defined in a function, the kernel. A kernel launch creates a grid of blocks, and each block has one or more threads. The organization of the grids and blocks can be 1D, 2D, or 3D.

During the running of the kernel:

Threads in the same block are executed simultaneously.
Blocks are scheduled by the streaming multiprocessors.

The NVIDIA Tesla C2050 has 14 streaming multiprocessors and threads are executed in groups of 32 (the warp size). This implies: \(14 \times 32 = 448\) threads can run simultaneously. For the K20C the numbers are respectively 13, 192, and 2496; and for the P100, we have respectively 56, 64, and 3584. A picture of the scalable programming model was shown in Fig. 87.

All threads execute the same code, defined by the kernel. The builtin variable threadIdx

identifies every thread in a block uniquely; and
defines the data processed by the thread.

The builtin variable blockDim holds the number of threads in a block. In a one dimensional organization, we use only threadIdx.x and blockDim.x. For 2D and 3D, the other components

threadIdx.y belongs to the range 0 .. blockDim.y;
threadIdx.z belongs to the range 0 .. blockDim.z.

The grid consists of N blocks, with \({\tt blockIdx.x} \in \{0,N-1\}\). Within each block, \({\tt threadIdx.x} \in \{ 0, {\tt blockDim.x}-1\}\). The organization of the data for each thread is in Fig. 95.

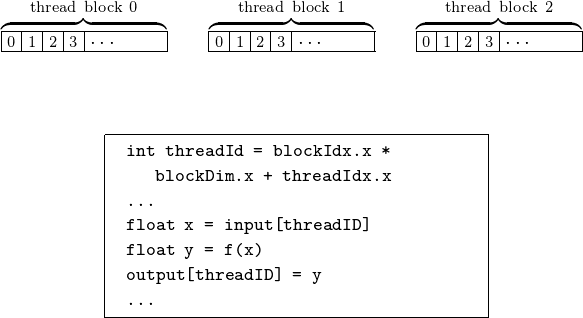
Fig. 95 Data mapped to threads with block and thread indices.

Suppose the kernel is defined by the function F with input arguments x and output arguments y, then the execution configuration parameters are set as below:

dim3 dimGrid(128,1,1);
dim3 dimBlock(32,1,1);
F<<<dimGrid,dimBlock>>>(x,y);

which launches a grid of 128 blocks. The grid is a one dimensional array. Each block in the grid is also one dimensional and has 32 threads.

begin{frame}{multidimensional thread organization}

The limitations of the Tesla C2050/C2070 are as follows:

Maximum number of threads per block: 1,024.
Maximum sizes of each dimension of a block: \(1,024 \times 1,024 \times 64\).

Because 1,024 is the upper limit for the number of threads in a block, the largest square 2D block is \(32 \times 32\), as \(32^2 = 1,024\).
Maximum sizes of each dimension of a grid: \(65,535 \times 65,535 \times 65,535\).

65,535 is the upper limit for the builtin variables gridDim.x, gridDim.y, and gridDim.z.

On the K20C and the P100, the limitations are as follows:

Maximum number of threads per block: 1,024.
Maximum dimension size of a thread block: \(1,024 \times 1,024 \times 64\).
Maximum dimension size of a grid size: \(2,147,483,647 \times 65,535 \times 65,535\).

Consider the following 3D example. Suppose the function F defines the kernel, with argument x, then

dim3 dimGrid(3,2,4);
dim3 dimBlock(5,6,2);
F<<<dimGrid,dimBlock>>>(x);

launches a grid with

\(3 \times 2 \times 4\) blocks; and
each block has \(5 \times 6 \times 2\) threads.

Matrix Matrix Multiplication¶

With a three dimensional grid we can define submatrices. Consider for example a grid of dimension \(2 \times 2 \times 1\) to store a 4-by-4 matrix in tiles of dimensions \(2 \times 2 \times 1\), as in Fig. 96.

Fig. 96 Storing a tiled matrix in a grid.

A kernel launch with a grid of dimensions \(2 \times 2 \times 1\) where each block has dimensions \(2 \times 2 \times 1\) creates 16 threads. The mapping of the entries in the matrix to threads is illustrated in Fig. 97.

Fig. 97 Mapping threads to entries in the matrix.

A kernel launch with a grid of dimensions \(2 \times 2 \times 1\) where each block has dimensions \(2 \times 2 \times 1\) creates 16 threads. The linear address calculation is illustrated in Fig. 98.

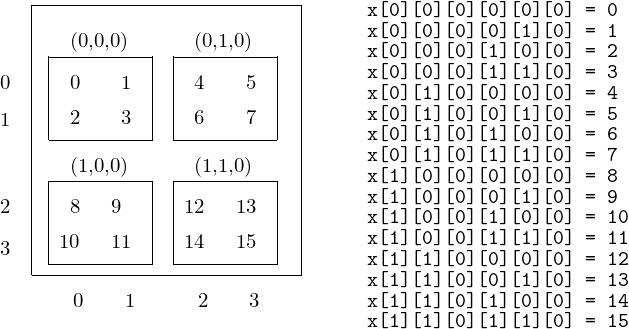
Fig. 98 Linear address calculation for threads and submatrices.

The main function in the CUDA code to organized the threads is listed below.

int main ( int argc, char* argv[] )
{
   const int xb = 2; /* gridDim.x */
   const int yb = 2; /* gridDim.y */
   const int zb = 1; /* gridDim.z */
   const int xt = 2; /* blockDim.x */
   const int yt = 2; /* blockDim.y */
   const int zt = 1; /* blockDim.z */
   const int n = xb*yb*zb*xt*yt*zt;

   printf("allocating array of length %d...\n",n);

   /* allocating and initializing on the host */

   int *xhost = (int*)calloc(n,sizeof(int));
   for(int i=0; i<n; i++) xhost[i] = -1.0;

   /* copy to device and kernel launch */

   int *xdevice;
   size_t sx = n*sizeof(int);
   cudaMalloc((void**)&xdevice,sx);
   cudaMemcpy(xdevice,xhost,sx,cudaMemcpyHostToDevice);

   /* set the execution configuration for the kernel */

   dim3 dimGrid(xb,yb,zb);
   dim3 dimBlock(xt,yt,zt);
   matrixFill<<<dimGrid,dimBlock>>>(xdevice);

The kernel is defined in the code below.

__global__ void matrixFill ( int *x )
/*
 * Fills the matrix using blockIdx and threadIdx. */
{
   int bx = blockIdx.x;
   int by = blockIdx.y;
   int tx = threadIdx.x;
   int ty = threadIdx.y;
   int row = by*blockDim.y + ty;
   int col = bx*blockDim.x + tx;
   int dim = gridDim.x*blockDim.x;
   int i = row*dim + col;
   x[i] = i;
}

Then the main program continues with the copying to host and writing the result.

   /* copy data from device to host */
   cudaMemcpy(xhost,xdevice,sx,cudaMemcpyDeviceToHost);
   cudaFree(xdevice);

   int *p = xhost;
   for(int i1=0; i1 < xb; i1++)
     for(int i2=0; i2 < yb; i2++)
       for(int i3=0; i3 < zb; i3++)
         for(int i4=0; i4 < xt; i4++)
           for(int i5=0; i5 < yt; i5++)
              for(int i6=0; i6 < zt; i6++)
                printf("x[%d][%d][%d][%d][%d][%d] = %d\n",
                        i1,i2,i3,i4,i5,i6,*(p++));
   return 0;
}

In a block all threads run independently. CUDA allows threads in the same block to coordinate their activities using a barrier synchronization function: __syncthreads(). The thread executing __syncthreads() will be held at the calling location in the code until every thread in the block reaches the location. Placing a __syncthreads() ensures that all threads in a block have completed a task before moving on.

Consider the tiled matrix multiplication, as shown in Fig. 99.

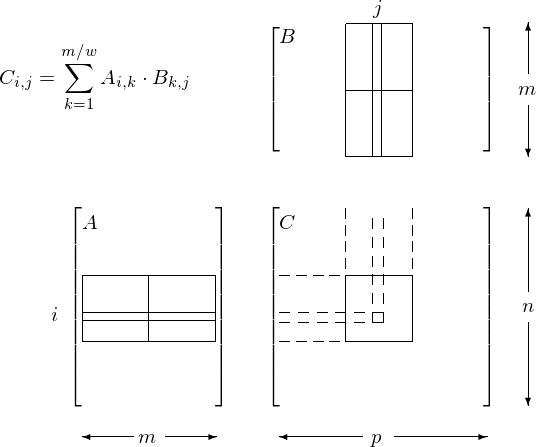
Fig. 99 Tiled matrix multiplication with shared memory.

With tiled matrix matrix multiplication using shared memory, all threads in the block collaborate to copy the tiles \(A_{i,k}\) and \(B_{k,j}\) from global memory to shared memory. Here is the need for thread synchronization. Before the calculation of the inner products, all threads must finish their copy statement: they all execute the __syncthreads(). Every thread computes one inner product. After this computation, another synchronization is needed. Before moving on to the next tile, all threads must finish, therefore, they all execute the __syncthreads() after computing their inner product and moving on to the next phase.

Let us then revisit the kernel of matrixMul and consider the code below.

template <int BLOCK_SIZE> __global__ void
matrixMul( float* C, float* A, float* B, int wA, int wB)
{
    int bx = blockIdx.x;   // Block index
    int by = blockIdx.y;
    int tx = threadIdx.x;  // Thread index
    int ty = threadIdx.y;
    // Index of the first sub-matrix of A processed by the block
    int aBegin = wA * BLOCK_SIZE * by;
    // Index of the last sub-matrix of A processed by the block
    int aEnd   = aBegin + wA - 1;
    // Step size used to iterate through the sub-matrices of A
    int aStep  = BLOCK_SIZE;
    // Index of the first sub-matrix of B processed by the block
    int bBegin = BLOCK_SIZE * bx;
    // Step size used to iterate through the sub-matrices of B
    int bStep  = BLOCK_SIZE * wB;

    // Csub is used to store the element of the block sub-matrix
    // that is computed by the thread
    float Csub = 0;

    // Loop over all the sub-matrices of A and B
    // required to compute the block sub-matrix
    for (int a = aBegin, b = bBegin;
             a <= aEnd;
             a += aStep, b += bStep) {

        // Declaration of the shared memory array As used to
        // store the sub-matrix of A
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];

        // Declaration of the shared memory array Bs used to
        // store the sub-matrix of B
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];

        // Load the matrices from device memory
        // to shared memory; each thread loads
        // one element of each matrix
        AS(ty, tx) = A[a + wA * ty + tx];
        BS(ty, tx) = B[b + wB * ty + tx];

        // Synchronize to make sure the matrices are loaded
        __syncthreads();

        // Multiply the two matrices together;
        // each thread computes one element
        // of the block sub-matrix
#pragma unroll
        for (int k = 0; k < BLOCK_SIZE; ++k)
            Csub += AS(ty, k) * BS(k, tx);

        // Synchronize to make sure that the preceding
        // computation is done before loading two new
        // sub-matrices of A and B in the next iteration
        __syncthreads();
    }

    // Write the block sub-matrix to device memory;
    // each thread writes one element
    int c = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
    C[c + wB * ty + tx] = Csub;
}

Bibliography¶

NVIDIA CUDA Programming Guide. Available at <http://developer.nvdia.com>.
Vasily Volkov and James W. Demmel: Benchmarking GPUs to tune dense linear algebra. In Proceedings of the 2008 ACM/IEEE conference on Supercomputing. IEEE Press, 2008. Article No. 31.

Exercises¶

Investigate the performance for the matrix-matrix multiplication with PyCUDA, comparing with the numpy implementation.
Find the limitations of the grid and block sizes for the graphics card on your laptop or desktop.
Extend the simple code with the three dimensional thread organization to a tiled matrix-vector multiplication for numbers generated at random as 0 or 1.

Thread Organization and Matrix Multiplication¶