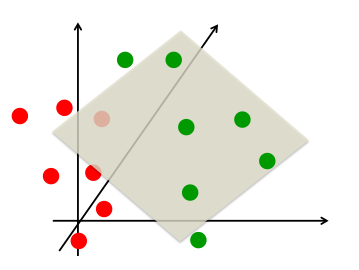

|
Syllabus: pdf |
| Time and Location: M-W-F 1:00pm - 1:50pm, Lincoln Hall (LH) 104 |
| Instructor Contact Information: Lev Reyzin, SEO 418, (312)-413-3745, | 
|
| Required Textbook: Mehryar Mohri, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of Machine Learning (available online via UIC library) |
| Optional Textbook: Shai Shalev-Shwartz and Shai Ben-David. Understanding Machine Learning: From Theory to Algorithms |
| Office Hours: M 10:00-10:50am, W 11:00-11:50am |