Determinantal Polynomials arising in Enumerative Geometry

Homotopies for solving problems in enumerative geometry appeared in [44]. The algorithms in the numerical Schubert calculus originated from questions in real enumerative geometry [96,97] and have their main application to the pole placement problem [12], [83,84], [88], [90] in control theory.

The enumerative problems are formalized in some ``finiteness'' theorems, avoiding the explicit but involved (as in (6)) formulas for the root counts.

Theorem 5.5   The number of r-planes meeting mr general m-planes in  ${\Bbb C}^{m+r}$is a finite constant.

The first homotopy presented in [44] uses a Gröbner basis for the ideal that defines G_mr, as is derived in [101]. By Gröbner bases questions concerning any polynomial system are solved by relation to monomial equations. Every Gröbner basis defines a flat deformation, which preserves the structure of the solution set [22]. Geometrically, this type of deformation is used to collapse the solution set in projective space to the coordinate hyperplanes, or in the opposite direction, to extend the solutions of the monomial equations to those of the original system. The flat deformations that are obtained in this way are similar to toric deformations in the sense that one moves from the solutions of a subsystem to the solutions of the whole system.

The Gröbner homotopies of [44] work in the synthetic Plücker embedding, and need to take the large set of defining equations of G_mr into account. When expanding the minors into local coordinates, these equations are automatically satisfied, which leads to a much smaller polynomial system. Consequently, the second type of homotopies of [44], the so-called SAGBI homotopies are more efficient. Instead of an ideal, we now have a subalgebra and work with a SAGBI basis, i.e.: the Subalgebra Analogue to a Gröbner Basis for an Ideal. The term order selects the monomials on the diagonal as the dominant ones. This implies that in the flat deformation (see [103] for a general description) only the diagonal monomials remain at t=0.

For m=2=r, the equations of the SAGBI homotopy in determinantal form are

$$p_i({\bf x}) = \det \left[ \left. \begin{array}{cc} c_{... ...& 0 \\ 0 & 1 \\ \end{array} \right] = 0, \quad i=1,2,3,4,$$ (30)

where the coefficients c_kl⁽ⁱ⁾ are random complex constants. In expanding the minors of (30), the lowest power of tis divided out, minor per minor. The system at t=0 is solved by polyhedral continuation. The system at t=1 serves as start system in the cheater's homotopy to solve any system with particular real values for the coefficients  c_kl⁽ⁱ⁾. Figure 10 outlines the structure of the general solver.

  

Figure 10: The SAGBI homotopy is at the center of the concatenation.

SAGBI homotopies have been implemented [114] to verify some large instances of input planes for which it was conjectured that all solution planes would be real. We refer to [89] and [98] for related work on these conjectures. In [99] an asymptotic choice of inputs is generated for which all solutions are proven to be real.

The third type of homotopies presented in [44] are the so-called Pieri homotopies. Since they are closer to the intrinsic geometric nature, they are applicable to a broader class of problems. In particular, we obtain an effective proof for the following.

Theorem 5.6   The number of r-planes meeting n general (m+1-k_i)-planes in  ${\Bbb C}^{m+r}$, with $k_1 + k_2 + \cdots + k_n = mr$, is a finite constant.

Note that when all k_i = 1, we arrive at Theorem 5.5. For general $k_i \not= 1$, we are not aware of any explicit formulas for the number of roots.

Figure 11 shows a part of a cellular decomposition of G₂₂ with the determinantal equations. We specialize the pattern X that represents a solution line by setting some of its coordinates to zero. This specialization determines a specialization of the input lines as follows: take those basis vectors not indexed by rows of Xwhere zeroes have been introduced. The special line S_X for this example is as in (31) spanned by the first and third standard basis vector.

  

Figure: Part of a cellular decomposition of the Grassmannian of all 2-planes. At the right we have the short-hand notation with brackets. The bracket [2 4] contains the row indices to the lowest nonzero entries in X.

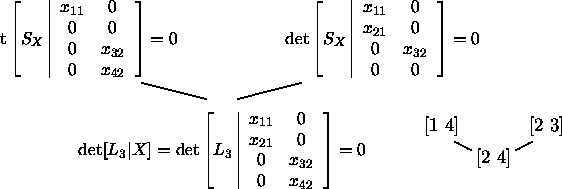Figure 11 pictures patterns of the moving 2-planes in the Pieri homotopy algorithm for the case (m,r) = (2,2), see Figure 6. The bottom matrix is the general representation of a solution that intersects already the two input lines spanned by the standard basis vectors. At the leaves of the tree by linear algebra operations we can intersect with a third input line. Moving down the poset, we deform form the left configuration in Figure 6 to the general problem.

Denote by L₁ and L₂ the lines already met by X. At the leaves of the tree in Figure 11 we intersect with the fourth line L₄. The special position for the third line L₃ is represented by the matrix S_X, which intersects any X with coordinates as at the leaves of the tree. In the homotopy $H(X,t) = {\bf0}$ we deform the line spanned by the columns of S_X to line L₃, for t = 0 to t = 1.

$$S_X = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & ... ...L_3 \vert X ) = 0 \\ \end{array} \right. \quad t \in [0,1].$$ (31)

Every solution X(t) of $H(X(t),t) = {\bf0}$ intersects already three lines: L₁, L₂ and L₃. At the end, for t=1, X also meets the line L₃ in a point.

The homotopy (31) deforms two solution lines, starting at patterns which have their row indices for the lowest nonzero entries respectively as in [1 4] and in [2 3]. The correctness of this homotopy (proven in [44] and [46]) justifies the formal root count using the localization poset. This combinatorial root count proceeds in two stages. First we build up the poset, from the bottom up, diminishing the entries in the brackets under the restriction that the same entry never occurs twice or more. Secondly, we descend from the top of the poset, collecting and adding up the counts at the nodes in the poset. More examples and variations are in [46].

To solve the general intersection problem of Theorem 5.6, the special (m+1-k_i)-planes lie in the intersection of special m-planes. In the construction of the poset one has to follow additional rules as to ensure a solution that meets the intersection of special m-planes. We refer to [46] for details.

The third enumerative problem we can solve is formalized as follows.

Theorem 5.7   The number of all maps of degree q that produce r-planes in ${\Bbb C}^{m+r}$meeting mr + q(m+r) general m-planes at specified interpolation points is a finite constant.

In [83,84] and [122] explicit formulas are given for this finite constant along with other combinatorial identities. Following a hint of Frank Sottile (see also [100]) and reverse engineering on the root counts in [83], Pieri homotopies were developed in [46] whose correctness yields a proof for Theorem 5.7.

The analogue to Figure 11 for maps of degree one into G₂₂ is displayed in Figure 12.

  

Figure 12: Part of a cellular decomposition of the Grassmannian of maps of degree 1 that produce 2-planes in projective 3-space. The bracket notation at the right corresponds to a matrix representation of the coefficients of the map X(s,t).

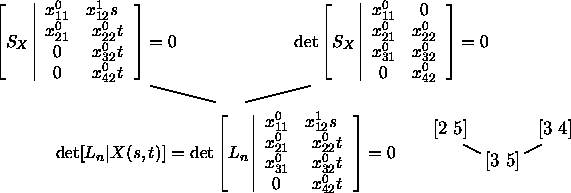To solve the problem in Theorem 5.7 we need a special position for the interpolation points. By moving those to infinity, the dominant monomials in the maps allow to re-use the same special m-planes, whose entries should be considered modulo m+r. The homotopy to satisfy the n-th intersection condition is:

$$H(X(s,t),s,t) = \left\{ \begin{array}{rl} \det(L_i \vert... ... (s-1)(1-t) + (s-s_n)t = 0 & t \in [0,1] \end{array} \right.$$ (32)

Note that the continuation parameter t moves the interpolation point from infinity, at (s,t) = (1,0), to the specific value (s,t) = (s_n,1).

See [100] for information on the selection of the input planes so that all maps are real.

As an example of another problem in enumerative geometry we mention the 27 lines on a cubic surface in 3-space. According to [81], this is one of the gems hidden in the rag-bag of projective geometry. In [92], the 27 lines are determined by breaking up the cubic surface into three planes in a continuous way such that each intermediate position is nonsingular. It is shown that this continuous variation is also valid in the real field.