The simplest system in the polytope model that still has isolated solutions
in
![]() has exactly two terms in every equation.
Polyhedral homotopies [40] solve systems with random complex
coefficients starting from sparser subsystems. For (2),
the homotopy with supports
has exactly two terms in every equation.
Polyhedral homotopies [40] solve systems with random complex
coefficients starting from sparser subsystems. For (2),
the homotopy with supports
![]() as in (16) is
as in (16) is
To find the start systems, we look at Figure 8,
at the subdivision that is induced by this lifting process.
The start systems have Newton polytopes spanned by one edge of the first
and one edge of the second polytope.
Since the two cells that contribute to the mixed volume
are characterized by their inner normals ![]() and
and ![]() satisfying (17) we denote the start systems respectively
by
satisfying (17) we denote the start systems respectively
by ![]() and
and ![]() .
To compute start solutions, unimodular transformations make the
system triangular as follows.
After dividing the equations so that the constant term is present,
we apply the substitution x1 = y2,
x2 = y1-1 y23 on
.
To compute start solutions, unimodular transformations make the
system triangular as follows.
After dividing the equations so that the constant term is present,
we apply the substitution x1 = y2,
x2 = y1-1 y23 on
![]() as follows:
as follows:
The substitution in (22) is apparent in the notation
(as used in [64])
![]() elaborated as
elaborated as
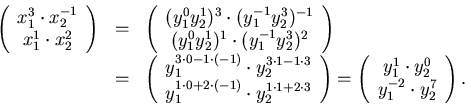 |
(23) |
![\begin{displaymath}\left[ \begin{array}{rr}
3 & -1 \\ 1 & 2
\end{array} \right...
...eft[ \begin{array}{rr}
1 & 0 \\ -2 & 7
\end{array} \right] .
\end{displaymath}](img178.gif) |
(24) |
The polyhedral homotopy (21) directly extends
the solutions of
![]() to the target system.
To obtain a homotopy starting
at the solutions of
to the target system.
To obtain a homotopy starting
at the solutions of ![]() ,
we substitute in (21)
,
we substitute in (21)
![]() ,
,
![]() and clear out the lowest powers of t.
This construction appeared in [40] and provides an algorithmic
proof of the following theorem.
and clear out the lowest powers of t.
This construction appeared in [40] and provides an algorithmic
proof of the following theorem.
For the numerical stability of polyhedral continuation, it is important to have subdivisions induced by low lifting values, since those influence the power of the continuation parameter. In [112] explicit lower bounds on integer lifting values were derived, but unfortunately the dynamic lifting algorithm does not generalize that well [65] if one is only interested in the mixed cells of a mixed subdivision. A balancing method was proposed in [30] to improve the stability of homotopies induced by random floating-point lifting values.
Once all solutions to a polynomial system with randomly generated coefficients are computed, we use cheater's homotopy to solve any specific system with the same Newton polytopes. One could say that polyhedral homotopies have removed the cheating part. The main advantage of polyhedral methods is that the mixed volume is a much sharper root count in most applications, leading to fewer paths to trace. They also allow more flexibility to exploit symmetry as demonstrated in [108].
In case the system has fewer isolated solutions than the mixed volume,
we consider the face systems. Define the face of a
polynomial p with support A as follows:
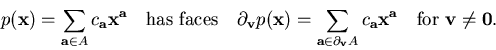 |
(25) |
In the polyhedral end game [43] solution paths are represented
by power series expansions:
To check whether a solution path really diverges is equivalent to
the test on the value for vi. A first-order approximation
of vi can be computed by
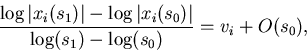 |
(27) |
| ei(k) | = | (28) | |
| = | c1 hk/m s0 (1 + O(hk/m)). | (29) |
Recall that
![]() count the roots in
count the roots in
![]() .
Using Newton polytopes to count affine roots
(i.e.: in
.
Using Newton polytopes to count affine roots
(i.e.: in
![]() instead of
instead of
![]() )
was proposed in [85] with the notion of shadowed polytopes obtained by
the substitution
)
was proposed in [85] with the notion of shadowed polytopes obtained by
the substitution
![]() for arbitrary constants ci.
To arrive at sharper bounds, it suffices (see [62] and [86])
to add a random constant to every equation.
Stable mixed volumes [42] provide a generically sharp affine root count.
The constructions in [26] and [29] avoid the use of
recursive liftings to compute stable mixed volumes.
Further developments and generalizations can be found in [87].
for arbitrary constants ci.
To arrive at sharper bounds, it suffices (see [62] and [86])
to add a random constant to every equation.
Stable mixed volumes [42] provide a generically sharp affine root count.
The constructions in [26] and [29] avoid the use of
recursive liftings to compute stable mixed volumes.
Further developments and generalizations can be found in [87].