Publications
Papers
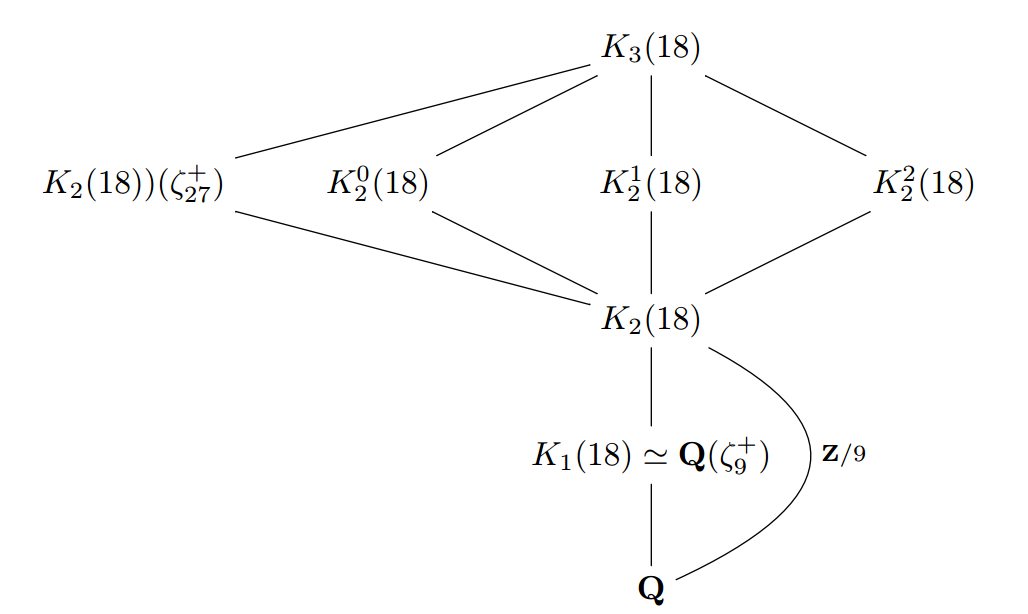
PDF Specializations of Generalized Rikuna Polynomials
with C. Cass, J. Cullinan and A. Rasmussen
International Journal of Number Theory 10, 585 (2014)
The generalized Rikuna polynomials are an iterative generalization of Rikuna's generic cyclic polynomials, which themselves generalize Shanks' cubic polynomials. In this paper we study Galois properties of the generalized Rikuna polynomials under specialization.
Other
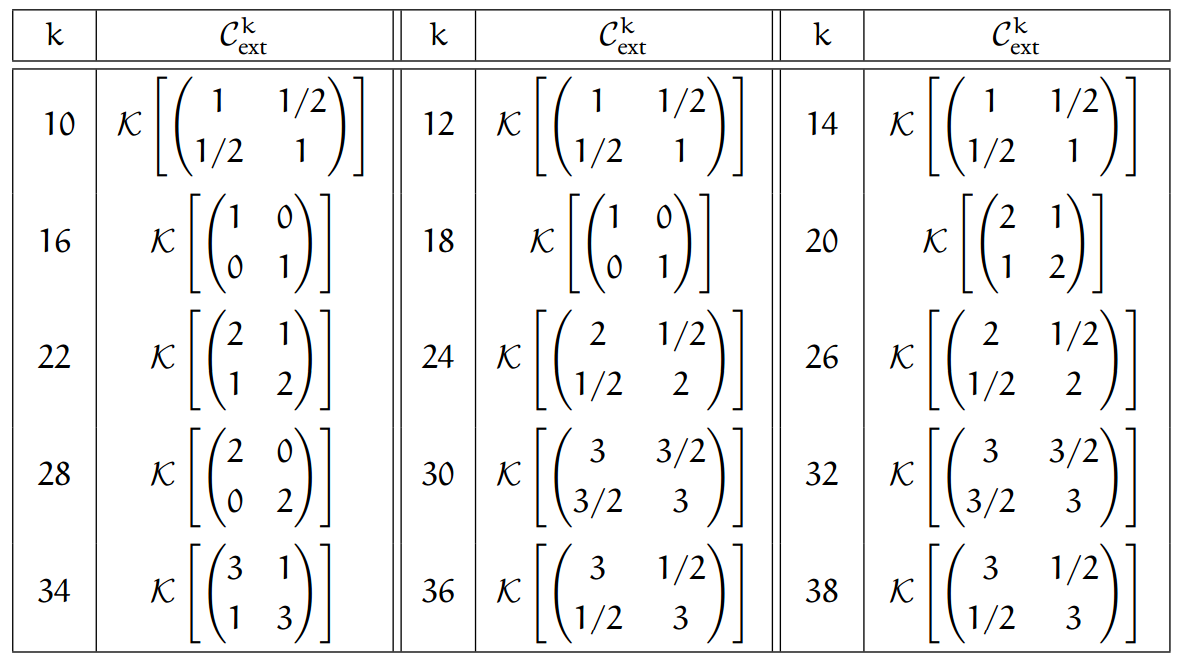
PDF Sage Computing the Extreme Core of Siegel Modular Forms
Undergraduate Thesis
The extreme core intrinsically characterises a nonvanishing set for the coefficients of the Fourier series of Siegel cusp forms, generalizing the valence inequality from the theory of classical modular forms. We give an algorithm for computing the extreme core when n = 2 for a fixed weight k and show that an estimate for the extreme core due to Cris Poor and David S. Yuen is optimal for cusp forms of even weight between 10 and 44.