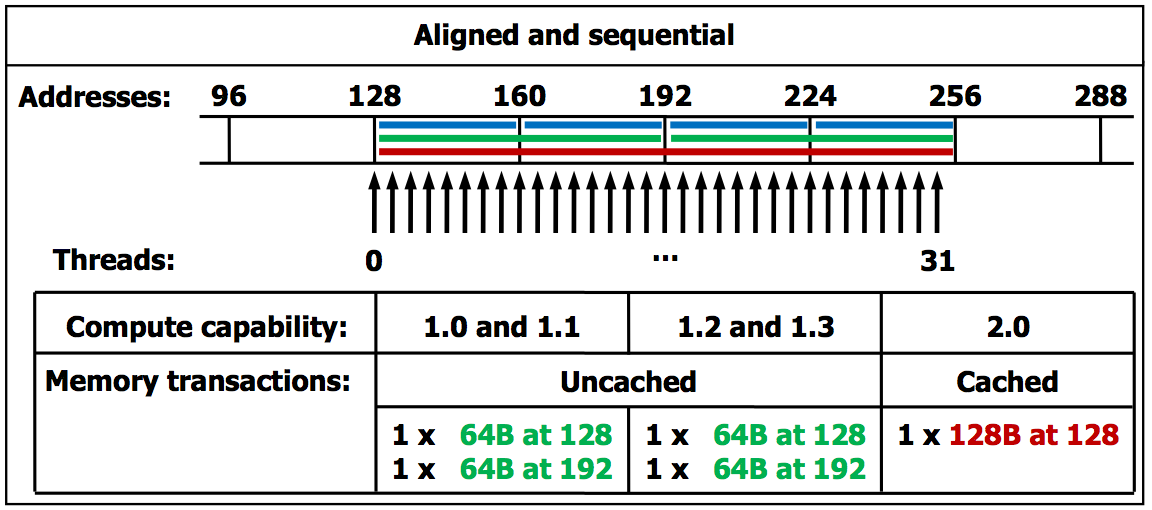
Memory Coalescing Techniques

To take full advantage of the high memory bandwidth of the GPU, the reading from global memory must also run in parallel. We consider memory coalescing techniques to organize the execution of load instructions by a warp.

Accessing Global and Shared Memory

Accessing data in the global memory is critical to the performance of a CUDA application. In addition to tiling techniques utilizing shared memories we discuss memory coalescing techniques to move data efficiently from global memory into shared memory and registers. Global memory is implemented with dynamic random access memories (DRAMs). Reading one DRAM is a very slow process.

Modern DRAMs use a parallel process: Each time a location is accessed, many consecutive locations that includes the requested location are accessed. If an application uses data from consecutive locations before moving on to other locations, the DRAMs work close to the advertised peak global memory bandwidth.

Recall that all threads in a warp execute the same instruction. When all threads in a warp execute a load instruction, the hardware detects whether the threads access consecutive memory locations. The most favorable global memory access is achieved when the same instruction for all threads in a warp accesses global memory locations. In this favorable case, the hardware coalesces all memory accesses into a consolidated access to consecutive DRAM locations.

If thread 0 accesses location \(n\), thread 1 accesses location \(n+1\), \(\ldots\) thread 31 accesses location \(n+31\), then all these accesses are coalesced, that is: combined into one single access.

The CUDA C Best Practices Guide gives a high priority recommendation to coalesced access to global memory. An example is shown in Fig. 104, extracted from Figure G-1 of the NVIDIA Programming Guide.

Fig. 104 An example of a global memory access by a warp.

More recent examples from the 2016 NVIDIA Programming guide are in Fig. 105 and Fig. 106.

Fig. 105 An example of aligned memory access by a warp.

Fig. 106 An example of mis-aligned memory access by a warp.

In /usr/local/cuda/include/vector_types.h we find the definition of the type double2 as

struct __device_builtin__ __builtin_align__(16) double2
{
    double x, y;
};

The __align__(16) causes the doubles in double2 to be 16-byte or 128-bit aligned. Using the double2 type for the real and imaginary part of a complex number allows for coalesced memory access.

With a simple copy kernel we can explore what happens when access to global memory is misaligned:

__global__ void copyKernel
 ( float *output, float *input, int offset )
{
   int i = blockIdx.x*blockDim.x + threadIdx.x + offset;
   output[i] = input[i];
}

The bandwidth will decrease significantly for offset \(> 1\).

avoiding bank conflicts in shared memory

Shared memory has 32 banks that are organized such that successive 32-bit words are assigned to successive banks, i.e.: interleaved. The bandwidth of shared memory is 32 bits per bank per clock cycle. Because shared memory is on chip, uncached shared memory latency is roughly 100 times slower than global memory.

A bank conflict occurs if two or more threads access any bytes within different 32-bit words belonging to the same bank. If two or more threads access any bytes within the same 32-bit word, then there is no bank conflict between these threads. The CUDA C Best Practices Guide gives a medium priority recommendation to shared memory access without bank conflicts.

Memory accesses are illustrated in Fig. 107 and Fig. 108.

Fig. 107 Examples of strided shared memory accesses, copied from Figure G-2 of the NVIDIA Programming Guide.

Fig. 108 Irregular and colliding shared memory accesses, is Figure G-3 of the NVIDIA Programming Guide.

Memory Coalescing Techniques

Consider two ways of accessing the elements in a matrix: * elements are accessed row after row; or * elements are accessed column after column.

These two ways are shown in Fig. 109.

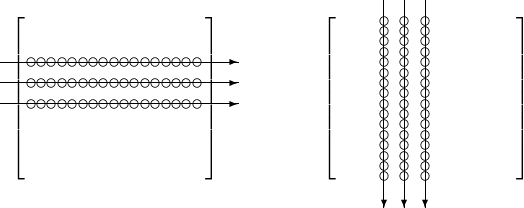
Fig. 109 Two ways of accessing elements in a matrix.

Recall the linear address system to store a matrix. In C, the matrix is stored row wise as a one dimensional array, see Fig. 90.

Threads \(t_0, t_1, t_2\), and \(t_3\) access the elements on the first two columns, as shown in Fig. 110.

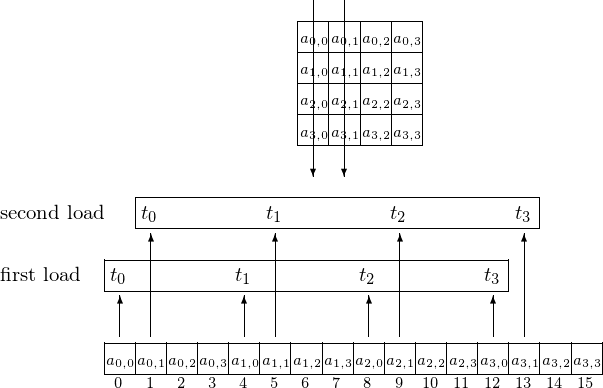
Fig. 110 Accessing elements column after column.

Four threads \(t_0, t_1, t_2\), and \(t_3\) access elements on the first two rows, as shown in Fig. 111.

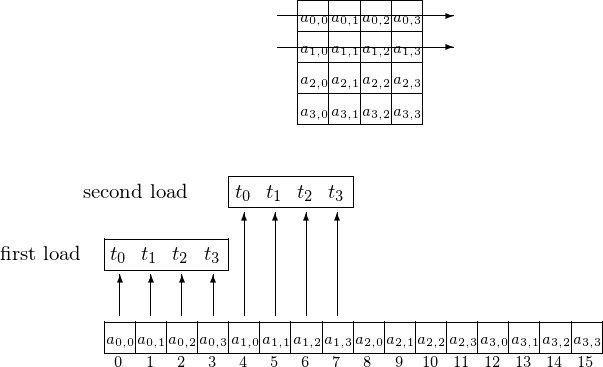
Fig. 111 Accesing elements row after row.

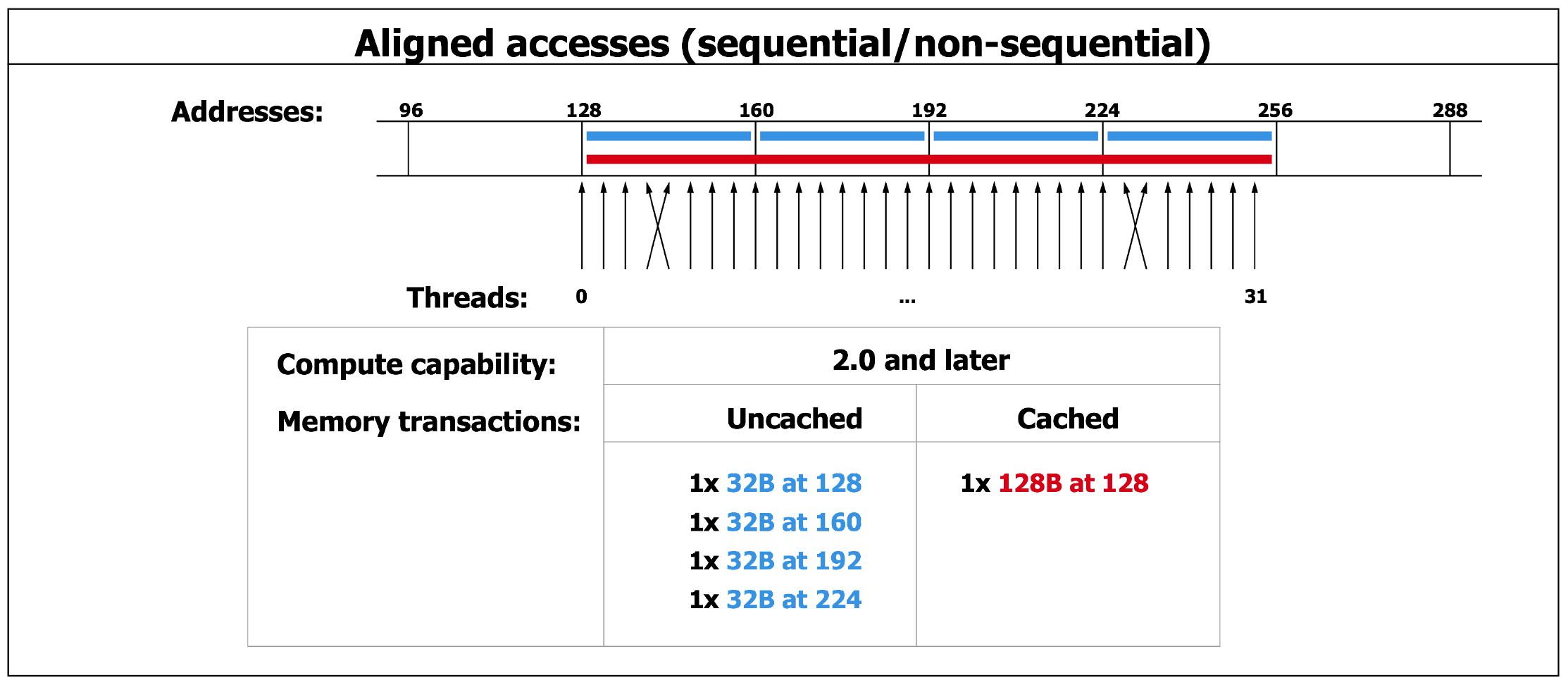
The differences between uncoalesced and coalesced memory accesses are shown in Fig. 112.

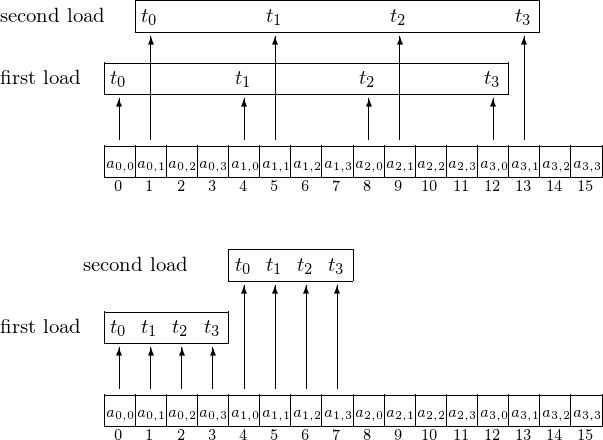
Fig. 112 Uncoalesced versus coalesced access.

We can use shared memory for coalescing. Consider Fig. 99 for the tiled matrix-matrix multiplication.

For \(\displaystyle C_{i,j} = \sum_{k=1}^{m/w} A_{i,k} \cdot B_{k,j}\), \(A \in {\mathbb R}^{n \times m}\), \(B \in {\mathbb R}^{m \times p}\), \(A_{i,k}, B_{k,j}, C_{i,j} \in {\mathbb R}^{w \times w}\), every warp reads one tile \(A_{i,k}\) of \(A\) and one tile \(B_{k,j}\) of \(B\): every thread in the warp reads one element of \(A_{i,k}\) and one element of \(B_{k,j}\).

The number of threads equals w, the width of one tile, and threads are identified with tx = threadIdx.x and ty = threadIdx.y. The by = blockIdx.y and bx = blockIdx.x correspond respectively to the first and the second index of each tile, so we have row = by* w + ty and col = bx* w + tx.

Row wise access to A uses A [row*m + (k*w + tx)]. For B: B [(k*w+ty)*m + col] = B [(k*w+ty)*m + bx*w+tx]. Adjacent threads in a warp have adjacent tx values so we have coalesced access also to B.

The tiled matrix multiplication kernel is below:

__global__ void mul ( float *A, float *B, float *C, int m )
{
   __shared__ float As[w][w];
   __shared__ float Bs[w][w];
   int bx = blockIdx.x;        int by = blockIdx.y;
   int tx = threadIdx.x;       int ty = threadIdx.y;
   int col = bx*w + tx;        int row = by*w + ty;
   float Cv = 0.0;
   for(int k=0; k<m/w; k++)
   {
      As[ty][tx] = A[row*m + (k*w + tx)];
      Bs[ty][tx] = B[(k*w + ty)*m + col];
      __syncthreads();
      for(int ell=0; ell<w; ell++)
         Cv += As[ty][ell]*Bs[ell][tx];
      C[row][col] = Cv;
   }
}

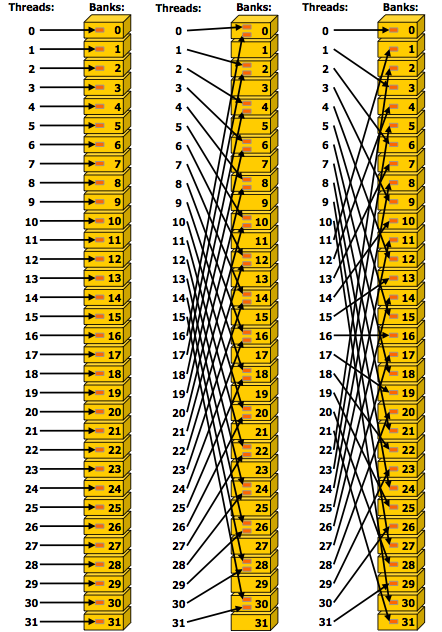
Avoiding Bank Conflicts

Consider the following problem:

On input are \(x_0, x_1, x_2, \ldots x_{31}\), all of type float.

The output is

\[\begin{split}\begin{array}{ccccc} x_0^2, & x_0^3, & x_0^4, & \ldots, & x_0^{33}, \\ x_1^2, & x_1^3, & x_1^4, & \ldots, & x_1^{33}, \\ x_2^2, & x_2^3, & x_2^4, & \ldots, & x_2^{33}, \\ \vdots & \vdots & \vdots & & \vdots \\ x_{31}^2, & x_{31}^3, & x_{31}^4, & \ldots, & x_{31}^{33}. \end{array}\end{split}\]

This gives 32 threads in a warp 1,024 multiplications to do. Assume the input and output resides in shared memory. How to compute without bank conflicts?

Suppose we observe the order of the output sequence. If thread \(i\) computes \(x_i^2, x_i^3, x_i^4, \ldots, x_i^{33}\), then after the first step, all threads write \(x_0^2, x_1^2, x_2^2, \ldots, x_{31}^2\) to shared memory. If the stride is 32, all threads write into the same bank. Instead of a simultaneous computation of 32 powers at once, the writing to shared memory will be serialized.

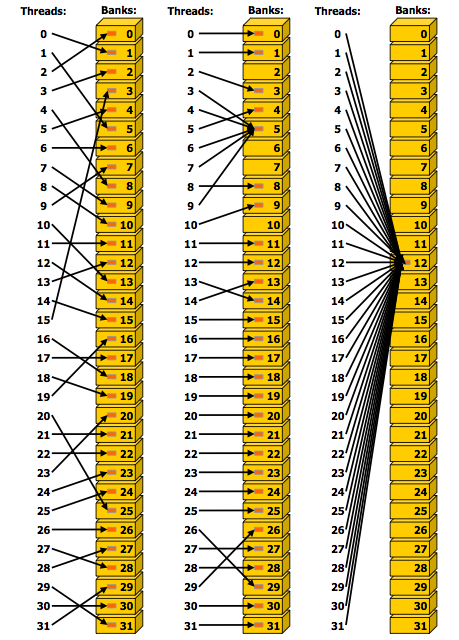
Suppose we alter the order in the output sequence.

\[\begin{split}\begin{array}{ccccc} x_0^2, & x_1^2, & x_1^2, & \ldots, & x_{31}^2, \\ x_0^3, & x_1^3, & x_2^3, & \ldots, & x_{31}^3, \\ x_0^4, & x_1^4, & x_2^4, & \ldots, & x_{31}^4, \\ \vdots & \vdots & \vdots & & \vdots \\ x_0^{33}, & x_1^{33}, & x_2^{33}, & \ldots, & x_{31}^{33}. \end{array}\end{split}\]

After the first step, thread \(i\) writes \(x_i^2\) in adjacent memory, next to \(x_{i-1}^2\) (if \(i > 0\)) and \(x_{i+1}^2\) (if \(i < 31\)). Without bank conflicts, the speedup will be close to 32.

Exercises

1. Run copyKernel for large enough arrays for zero offset and an offset equal to two. Measure the timings and deduce the differences in memory bandwidth between the two different values for offset.
2. Consider the kernel of matrixMul in the GPU computing SDK. Is the loading of the tiles into shared memory coalesced? Justify your answer.
3. Write a CUDA program for the computation of consecutive powers, using coalesced access of the values for the input elements. Compare the two orders of storing the output sequence in shared memory: once with and once without bank conflicts.