MCS 441 - Theory of Computation I
University of Illinois - Chicago
Spring 2014

This course will cover basic computability and complexity theory. We will examine the central questions ''What is computable in principle?" and ''What is efficiently computable?" Covered material will likely include, but not be limited to: automata, regular languages, and nondeterminism; context-free languages and pushdown automata; Turing machines and the Church-Turing thesis; decidability and the halting problem; Kolmogorov complexity; time complexity, P vs. NP, the Cook-Levin theorem, and reductions; and time permitting, PSPACE, L, NL, or other advanced topics.

Basic Information

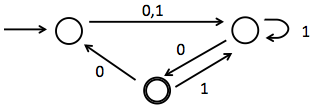
Syllabus: pdf
Time and Location: M-W-F 12:00-12:50pm, Taft Hall (TH) 219
Instructor Contact Information: Lev Reyzin, SEO 713, (312)-413-9576,
Textbook: M. Sipser, Introduction to the Theory of Computation, 3rd edition
Office Hours: M 11:00AM-11:50AM, R 10:00AM-10:50AM

Exam Dates

Midterm 1: 12:00-12:50 p.m. Friday, February 14, in class
Midterm 2: 12:00-12:50 p.m. Friday, April 4, in class
Final Exam: 8:00-10:00 a.m. Tuesday, May 6

Problem Sets

Problem Set 1 (pdf), due 2/5/14
Problem Set 2 (pdf), due 2/12/14
Problem Set 3 (pdf), due 3/5/14
Problem Set 4 (pdf), due 3/31/14 (Turing's paper and Aaronson's article)
Problem Set 5 (pdf), due 4/25/14

Lectures and Readings

Note: lectures will have material not covered in the readings.

Lecture 1 (1/13/14)
covered material: intro to the course, overview of prerequisite material
other: slides from class
reading: chapter 0

Lecture 2 (1/15/14)
covered material: intro to DFAs: examples, their formal description, defining computation
reading: begin chapter 1.1

Lecture 3 (1/18/14)
covered material: designing DFAs, the regular operations, closure under union
reading: finish chapter 1.1

Lecture 4 (1/22/14)
covered material: intro to NFAs, equivalence of NFAs and DFAs
reading: begin chapter 1.2

Lecture 5 (1/25/14)
covered material: more NFA examples, closure of RLs under concatenation and star
reading: finish chapter 1.2
other: problem set 1 assigned

Lecture 6 (1/27/14)
covered material: intro to regular expressions, converting REs to NFA, intro to GNFAs
reading: begin chapter 1.3

Lecture 7 (1/29/14)
covered material: showing REs equivalent to regular languages via GNFAs
reading: finish chapter 1.3

Lecture 8 (1/31/14)
covered material: non-regular languages, pumping lemma and its proof reading: chapter 1.4

Lecture 9 (2/3/14)
covered material: intro to CFGs and CFLs, their formal definition, that RLs are a proper subset of CFLs
reading: begin chapter 2.1

Lecture 10 (2/5/14)
covered material: ambiguous grammars, inherently ambiguous languages, Chomsky normal form
reading: continue chapter 2.1
other: problem set 2 assigned

Lecture 11 (2/7/14)
covered material: converting a CFG into CNF
reading: finish chapter 2.1
other: midterm 1 announced, to take place 2/14/14 in class

Lecture 12 (2/10/14)
covered material: intro to PDAs, their formal description and state diagrams, nondeterminism in PDAs
reading: begin chapter 2.2

Lecture 13 (2/12/14)
covered material: review for midterm
other: midterm Friday!

Lecture 14 (2/14/14)
midterm exam 1, no lecture

Lecture 15 (2/17/14)
covered material: more PDA examples
reading: continue chapter 2.2

Lecture 16 (2/21/14)
covered material: equivalence of CFGs and PDAs
reading: finish chapter 2.2

Lecture 17 (2/24/14)
covered material: pumping lemma for CFLs and its proof
reading: begin chapter 2.3
other: problem set 3 assigned

Lecture 18 (2/26/14)
covered material: more pumping lemma for CFL examples, CFL closure properties
reading: finish chapter 2.3

Lecture 19 (2/28/14)
covered material: intro to TMs, their formal description and state diagrams
reading: begin chapter 3.1

Lecture 20 (3/3/14)
covered material: TM examples, decidable and recognizable languages, multi-tape TMs
reading: finish chapter 3.1

Lecture 21 (3/5/14)
covered material: nondeberministic TMs and their equivalence to TMs
reading: begin chapter 3.2

Lecture 22 (3/7/14)
covered matherial: enumerators, Church-Turing thesis, intuitive idea of algorithms
reading: finish chapter 3.2, begin chapter 3.3

Lecture 23 (3/10/14)
covered material: encodings, ADFA, ANFA, AREX, EDFA, EQDFA, ACFG are all decidable, co-recognizability
reading: finish chapter 3.3, begin chapter 4.1

Lecture 24 (3/12/14)
covered material: ECFG is decidable, HALTTM is recognizable, diagonalization, ATM and HALTTM are not decidable.
reading: finish chapter 4.1, chapter 4.2

Lecture 25 (3/14/14)
covered material: introduction to reductions, ETM and EQTM not decidable, intro to mapping reductions
reading: beginning of chapter 5.1, begin chapter 5.3

Lecture 26 (3/17/14)
covered material: more on mapping reductions, ATM not co-recognizable, ATM not recognizable, EQTM is neither
reading: finish chapter 5.3
other: problem set 4 assigned

Lecture 27 (3/19/14)
covered material: Rice's theorem, Post Correspondence problem, introduction to Kolmogorov complexity
reading: skim chapter 5.2, begin chapter 6.4

Lecture 28 (3/21/14)
covered material: bounds on Kolmogorov complexity L(x), incomputability of K(x)
reading: finish chapter 6.4

Lecture 29 (3/31/14)
covered material: introduction to time complexity, examples for running times
reading: begin chapter 7.1

Lecture 30 (4/2/14)
covered material: asymptotic analysis and notation
reading: finish chapter 7.1
other: midterm Friday!

Lecture 31 (4/4/14)
midterm exam 2, no lecture

Lecture 32 (4/7/14)
covered material:the complexity theoretic Church-Turing thesis
reading: begin chapter 7.2

Lecture 33 (4/9/14)
covered material: the classes TIME(t(n)), NTIME(t(n)), P, NP, RELPRIME in P
reading: finish chapters 7.1 and chapter 7.2

Lecture 34 (4/11/14)
covered material: polynomial time verifiability and certificates, polynomial time verifier for COMPOSITES
reading: begin chapter 7.3

Lecture 35 (4/14/14)
covered material: equivalence of NP and deterministic verifiers, HAM-PATH and CLIQUE problems
reading: finish chapter 7.3

Lecture 36 (4/16/14)
covered material: polynomial time reductions, 3SAT
reading: begin chapter 7.4

Lecture 37 (4/18/14)
covered material NP-Completeness, example reduction, coNP
reading: continue chapter 7.4
other: problem set 5 assigned

Lecture 38 (4/21/14)
covered material: more reductions
reading: chapter 7.5

Lecture 39 (4/23/14)
covered material: Cook-Levin theorem
reading: finish chapter 7.4

Lecture 40 (4/25/14)
covered material: intro to space complexity, the classes SPACE and NSPACE
reading: begin chapter 8.1

Lecture 41 (4/28/14)
covered material: the class PSPACE, PSPACE = NPSPACE
reading: finish chapter 8.1, chapter 8.2

Lecture 42 (4/30/14)
covered material: PSPACE-Completeness, TQBF, polynomial heirarchy
reading: finish chapter 8.3

Lecture 43 (5/2/14)
covered material: time and space heirarchy theorems, L and NL
reading: read chapter 8.4