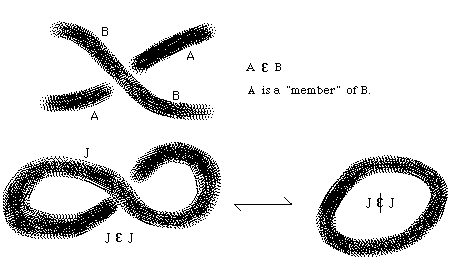
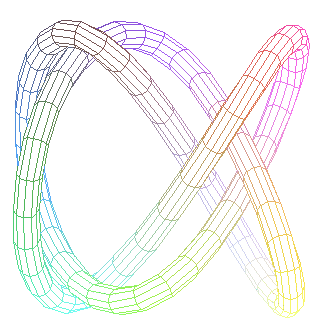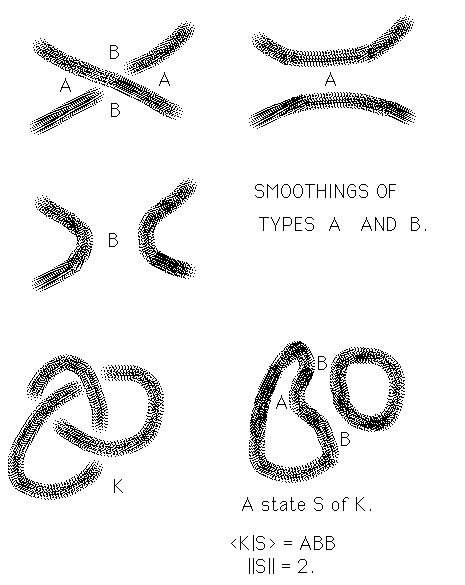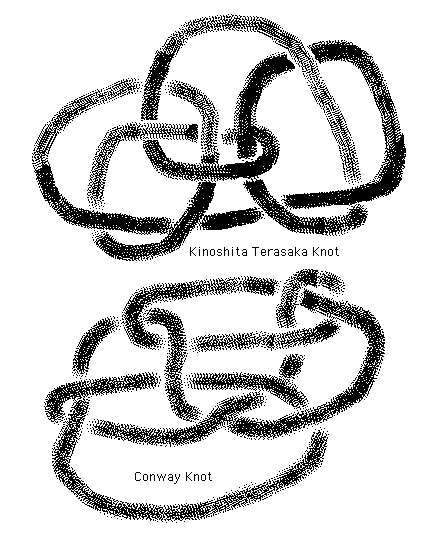New Teaching: Knot Theory - Fall 2018 See Knots
See BLOG.
Recent Teaching : Math 300 - Writing Mathematics - Spring 2017. See Writing!
Recent Teaching: Knot Theory - Spring 2017. See Knots
Introduction to Quantum Theory and Knots. See KnotPhysics
######################################################################################################################
FORM Papers on Form. FORM = FORM(DISTINCTION). "The form we take to exist arises from framing nothing." "We take the form of distinction for the form."
RD Recursive Distinctioning - Papers and Discussion.
See Box Algebra Exercise. This is an exercise in the writing course and it is an introduction to the mathematics of G. Spencer-Brown and Charles Sanders Peirce.
#############################################################################################
See Neslihan Gugumcu. This is beginning of a list of references to webpages of friends and collaborators.
########################################################################################################################
KNOTS. See MATH 569. (History: From September 1, 2003 to August 31, 2004 at the University of Waterloo and the Perimeter Institute in Waterloo, Canada. In July 2004, a workshop on knots and applications at the MSRI workshop at University of British Columbia in Vancouver, BC. Knot Theory in Trieste at the Abdus Salam International Centre for Theoretical Physics in May 2007. Jyvaskyla, Finland in August 2007. Trieste in May 2009. This link also applies to Math 569 for Spring 2007, Math 568 for Spring 2009 and Math 569 for Spring 2011 and Spring 2015 and Spring 2017.)
I taught : Math 467 - Elementary Number Theory - Fall 2016. See Number Theory.
I taught : Math 210 - Third Term Calculus - Spring 2016. See Calculus III.
I taught Math 313 - Mathematical Analysis I - in Fall 2014. See Analysis
I taught Math 442 - Differential Geometry - in Fall 2014. See Geometry
I taught Math 435 - Abstract Algebra - in Spring 2014. See Algebra
I taught Applied Linear Algebra, Math 310 in Fall 2013. See Vector Algebra.
I taught 215 - Introduction to Advanced Mathematics - in Spring 2013. See Proofs! for the course webpage. If you google "Eccles, An Introduction to Mathematical Reasoning", you will obtain information about the book for the course,
I taught Math 548 - Algebraic Topology - in Spring 2013. See Homology! for the course webpage.
I taught Calculus, Math 181 in Fall 2010. See Calculus.
I taught Math 423 - Graph Theory - in Spring 2010. See Graph Theory
I taught a course in knot theory and topological visualization. For some notes about knots in the the seven color map on the torus see the pdf file The Knot in the Seven Color Map.
See KNOTS IN CHICAGO, Sept 10-12, 2010.
Here is a collection of internal and external links.